Question

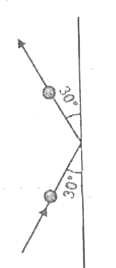
A ball moving with a momen - tum of ${\displaystyle 15kgm{s}^{-1}}$ strickes against the wall at an angle of ${\displaystyle {30}^{\circ }}$ and is reflected back with the same momentum at the same angle . Calculte impulse.

Explanation

To solve the problem step by step, we will calculate the impulse experienced by the ball when it strikes the wall at an angle of 30 degrees and reflects back with the same momentum.

Step 1: Understand the Problem
The ball has an initial momentum of \( P = 15 \, \text{kg m/s} \) and strikes the wall at an angle of \( 30^\circ \). After striking the wall, it reflects back with the same momentum at the same angle.

Step 2: Break Down the Momentum into Components
We need to resolve the momentum into two components: one parallel to the wall (horizontal component) and one perpendicular to the wall (vertical component).

- The component of momentum perpendicular to the wall (normal component):
\( P_{\text{normal}} = P \sin(30^\circ) \)

- The component of momentum parallel to the wall (tangential component):
\( P_{\text{tangential}} = P \cos(30^\circ) \)

Step 3: Calculate the Components
Using the values:
- \( P = 15 \, \text{kg m/s} \)
- \( \sin(30^\circ) = \frac{1}{2} \)
- \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \)

Calculating the components:
- Normal component:
\( P_{\text{normal}} = 15 \sin(30^\circ) = 15 \times \frac{1}{2} = 7.5 \, \text{kg m/s} \)

- Tangential component:
\( P_{\text{tangential}} = 15 \cos(30^\circ) = 15 \times \frac{\sqrt{3}}{2} = 15 \frac{\sqrt{3}}{2} \approx 12.99 \, \text{kg m/s} \)

Step 4: Determine the Change in Momentum
When the ball strikes the wall, the normal component of momentum changes direction (it becomes negative), while the tangential component remains unchanged.

- Initial momentum perpendicular to the wall:
\( P_{\text{initial}} = P_{\text{normal}} = 7.5 \, \text{kg m/s} \)

- Final momentum perpendicular to the wall (after reflection):
\( P_{\text{final}} = -P_{\text{normal}} = -7.5 \, \text{kg m/s} \)

Step 5: Calculate the Impulse
Impulse is defined as the change in momentum:
\( \text{Impulse} = \Delta P = P_{\text{final}} - P_{\text{initial}} \)
Substituting the values:
\( \text{Impulse} = (-7.5) - (7.5) = -15 \, \text{kg m/s} \)

Since impulse is a vector quantity, we can take the magnitude:
\( \text{Magnitude of Impulse} = 15 \, \text{kg m/s} \)

Step 6: Final Result
The impulse experienced by the ball is:
\( \text{Impulse} = 15 \, \text{kg m/s} \)

---