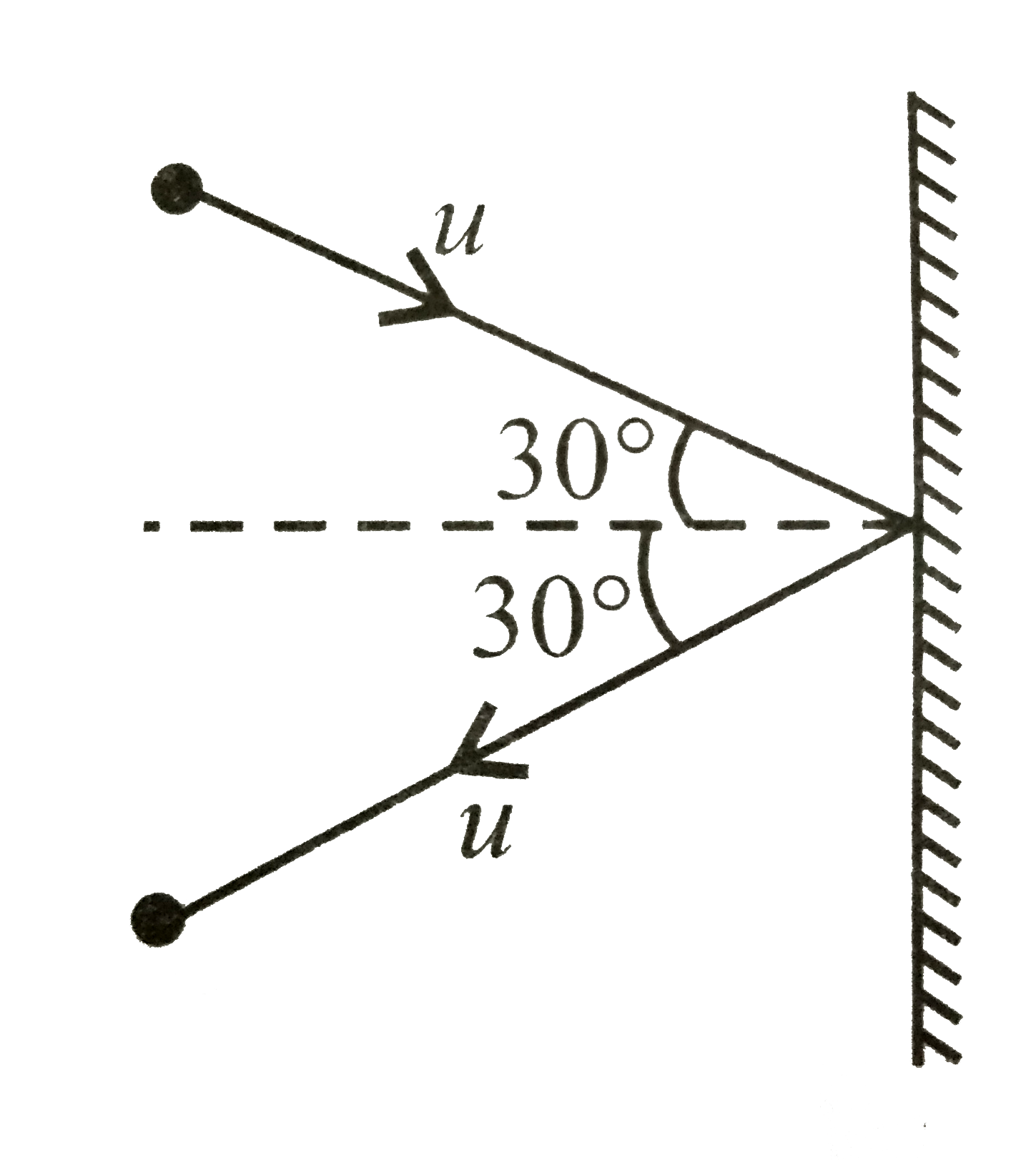
Two identical billiard balls striks a rigid wall with the same speed but at different angles , and get reflected without any change in speed , as shown in Fig . What is (i) the direction of the force on the wall due to each ball ? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
To solve the problem step by step, we will analyze the situation of two identical billiard balls striking a rigid wall at different angles and determine the direction of the force on the wall and the ratio of the impulses imparted to the balls by the wall.
Step 1: Understanding the Situation
We have two identical billiard balls striking a rigid wall with the same speed (let's denote it as u) but at different angles. When they strike the wall, they reflect without any change in speed.
Step 2: Analyzing the First Ball
Let’s consider the first ball striking the wall perpendicularly (at an angle of 0 degrees).
- The initial momentum of the ball before striking the wall is p1=mu (where m is the mass of the ball).
- After reflection, the momentum becomes p′1=−mu (the direction is reversed).
- The change in momentum (impulse) for the first ball is:
I1=p′1−p1=−mu−mu=−2mu
- The direction of the force on the wall due to the first ball is in the direction of the wall's normal (perpendicular to the wall).
Step 3: Analyzing the Second Ball
Now, consider the second ball striking the wall at an angle θ (let’s assume θ=30∘).
- The horizontal component of the velocity is ucos(30∘) and the vertical component is usin(30∘).
- The initial momentum components before striking the wall are:
- Horizontal: px1=mucos(30∘)
- Vertical: py1=musin(30∘)
- After reflection, the horizontal momentum becomes px2=−mucos(30∘) (the direction is reversed) and the vertical momentum remains the same.
- The change in momentum (impulse) for the second ball is:
I2=px2−px1=−mucos(30∘)−mucos(30∘)=−2mucos(30∘)
Step 4: Direction of Force on the Wall
- For both balls, the force exerted on the wall is directed inward (toward the wall) due to the change in momentum.
- Therefore, the direction of the force on the wall due to the first ball is normal to the wall, while for the second ball, it also has a horizontal component due to the angle of incidence.
Step 5: Ratio of Impulses
Now, we find the ratio of the magnitudes of impulses imparted to the balls by the wall:
Ratio=|I1||I2|=2mu2mucos(30∘)=1cos(30∘)
- Since cos(30∘)=√32, we have:
Ratio=1√32=2√3
Final Answers
1. Direction of the force on the wall due to each ball: The force is directed inward (normal to the wall) for both balls.
2. Ratio of the magnitudes of impulses: The ratio is 2√3.
We have two identical billiard balls striking a rigid wall with the same speed (let's denote it as u) but at different angles. When they strike the wall, they reflect without any change in speed.
Let’s consider the first ball striking the wall perpendicularly (at an angle of 0 degrees).
- The initial momentum of the ball before striking the wall is p1=mu (where m is the mass of the ball).
- After reflection, the momentum becomes p′1=−mu (the direction is reversed).
- The change in momentum (impulse) for the first ball is:
I1=p′1−p1=−mu−mu=−2mu
- The direction of the force on the wall due to the first ball is in the direction of the wall's normal (perpendicular to the wall).
Now, consider the second ball striking the wall at an angle θ (let’s assume θ=30∘).
- The horizontal component of the velocity is ucos(30∘) and the vertical component is usin(30∘).
- The initial momentum components before striking the wall are:
- Horizontal: px1=mucos(30∘)
- Vertical: py1=musin(30∘)
- After reflection, the horizontal momentum becomes px2=−mucos(30∘) (the direction is reversed) and the vertical momentum remains the same.
- The change in momentum (impulse) for the second ball is:
I2=px2−px1=−mucos(30∘)−mucos(30∘)=−2mucos(30∘)
- For both balls, the force exerted on the wall is directed inward (toward the wall) due to the change in momentum.
- Therefore, the direction of the force on the wall due to the first ball is normal to the wall, while for the second ball, it also has a horizontal component due to the angle of incidence.
Now, we find the ratio of the magnitudes of impulses imparted to the balls by the wall:
Ratio=|I1||I2|=2mu2mucos(30∘)=1cos(30∘)
- Since cos(30∘)=√32, we have:
Ratio=1√32=2√3
1. Direction of the force on the wall due to each ball: The force is directed inward (normal to the wall) for both balls.
2. Ratio of the magnitudes of impulses: The ratio is 2√3.
Topper's Solved these Questions
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:conceptual problmes
Explore 45 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Very short answer questions
Explore 73 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 NCERT Comprehension
Explore 4 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
Similar Questions
As shown in fig. two identical balls strike a rigid wall with equal speeds but a different angles of incidence. They are reflected back without any lose in speed.


(a) Determine the direction of force exerted by each ball on the wall.
(b) Determine the ratio of impulse imparted by the two balls on the wall in both cases.
View SolutionA ball of mass m strikes a rigid wall with speed v and gets reflected without any loss of speed, as shown in the figure.
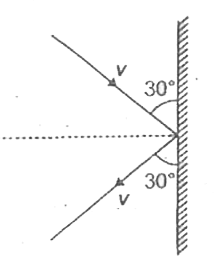
(a) What is the magnitude of the impulse imparted to the ball by the wall?
(b) What is the direction of the force on the wall due to the ball?
View Solution
Knowledge Check
A rigid ball of mass m strikes a rigid wall at 60∘ and gets reflected without loss of speed as shown in the figure. The value of impulse imparted by the wll on the ball will be
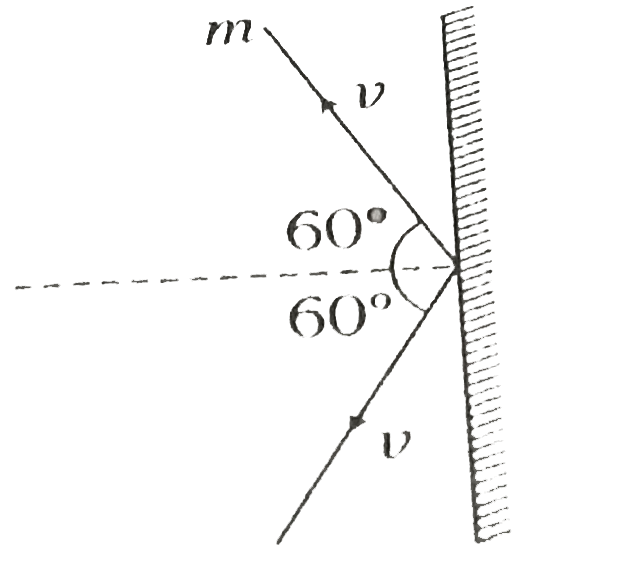 AmvB2mvCmv/2Dmv/3
AmvB2mvCmv/2Dmv/3A ball of mass 'm' strikes a rigid wall with speed 'u' and rebounds with the same speed. The impulse imparted to the ball by the wall is
A2 mu,Bmu,CzeroD−2mnA riding ball of mass m strikes a rigid wall at 60∘ and gets reflected without loss of speed as shown in the figure below. The value of impulse imparted by the wall on the ball will be.
 AmV2BmV3CmVD2mV
AmV2BmV3CmVD2mV
A particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
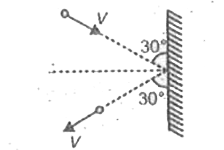
View SolutionTwo billiard balls of equal mass 30 g strike a rigid wall with same speed of 108 kmph (as shown) but at different angles. If the balls get reflected with the same speed then the ratio of the magnitude of impulses imparted to ball 'a' and ball 'b' by the wall along 'X' direction is
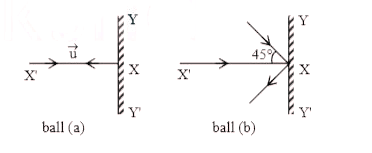
View SolutionA batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 15m/s.If the mass of ball is 0.1kg then impulse imparted to the ball will be
View SolutionA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
View SolutionA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
View Solution

