A body is of mass 1 kg falls freely from a height of 100 m. on a platform of mass 3 kg which is mounted on a spring having spring constant k=1.25×106N/m.The body sticks to the platform and the spring's maximum compression is found to be x .Given that g=10ms−2 ,the value of x will be close to :
40 cm
4 cm
80 cm
8 cm
To solve the problem of a body falling onto a platform mounted on a spring, we can follow these steps:
Step 1: Calculate the gravitational potential energy (PE) of the falling body
The gravitational potential energy of the body just before it hits the platform can be calculated using the formula:
PE=mgh
where:
- m=1kg (mass of the body)
- g=10m/s2 (acceleration due to gravity)
- h=100m (height from which it falls)
Calculating:
PE=1×10×100=1000J
Step 2: Determine the total mass after the collision
After the body sticks to the platform, the total mass M of the system (body + platform) is:
M=m+Mp=1kg+3kg=4kg
Step 3: Calculate the velocity of the system just before the spring compression
Using the conservation of energy, the potential energy of the falling body converts into kinetic energy (KE) just before it hits the platform:
KE=12Mv2
Setting the potential energy equal to the kinetic energy:
1000=12×4×v2
Solving for v2:
1000=2v2
v2=500
v=√500=10√5m/s
Step 4: Calculate the maximum compression of the spring
At maximum compression x, all kinetic energy will be converted into the potential energy of the spring:
KE=PEspring
12Mv2=12kx2
Substituting the values:
1000=12×1.25×106×x2
1000=625000x2
Solving for x2:
x2=1000625000
x2=1625
x=125=0.04m=4cm
Final Answer
The maximum compression x of the spring is approximately 4 cm.
---
The gravitational potential energy of the body just before it hits the platform can be calculated using the formula:
PE=mgh
where:
- m=1kg (mass of the body)
- g=10m/s2 (acceleration due to gravity)
- h=100m (height from which it falls)
PE=1×10×100=1000J
After the body sticks to the platform, the total mass M of the system (body + platform) is:
M=m+Mp=1kg+3kg=4kg
Using the conservation of energy, the potential energy of the falling body converts into kinetic energy (KE) just before it hits the platform:
KE=12Mv2
Setting the potential energy equal to the kinetic energy:
1000=12×4×v2
Solving for v2:
1000=2v2
v2=500
v=√500=10√5m/s
At maximum compression x, all kinetic energy will be converted into the potential energy of the spring:
KE=PEspring
12Mv2=12kx2
Substituting the values:
1000=12×1.25×106×x2
1000=625000x2
Solving for x2:
x2=1000625000
x2=1625
x=125=0.04m=4cm
The maximum compression x of the spring is approximately 4 cm.
Topper's Solved these Questions
- JEE MAINSBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINSExercise:Chemistry
Explore 1 Video
- JEE MAINBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINExercise:All Questions
Explore 452 Videos
- JEE MAINS 2020Book:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINS 2020Exercise:PHYSICS
Explore 250 Videos
Similar Questions
A body of mass 0.2 kg falls from a height of 10 m to a height of 6 m above the ground. Find the loss in potential energy taking place in the body.
[g=10ms−2]
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
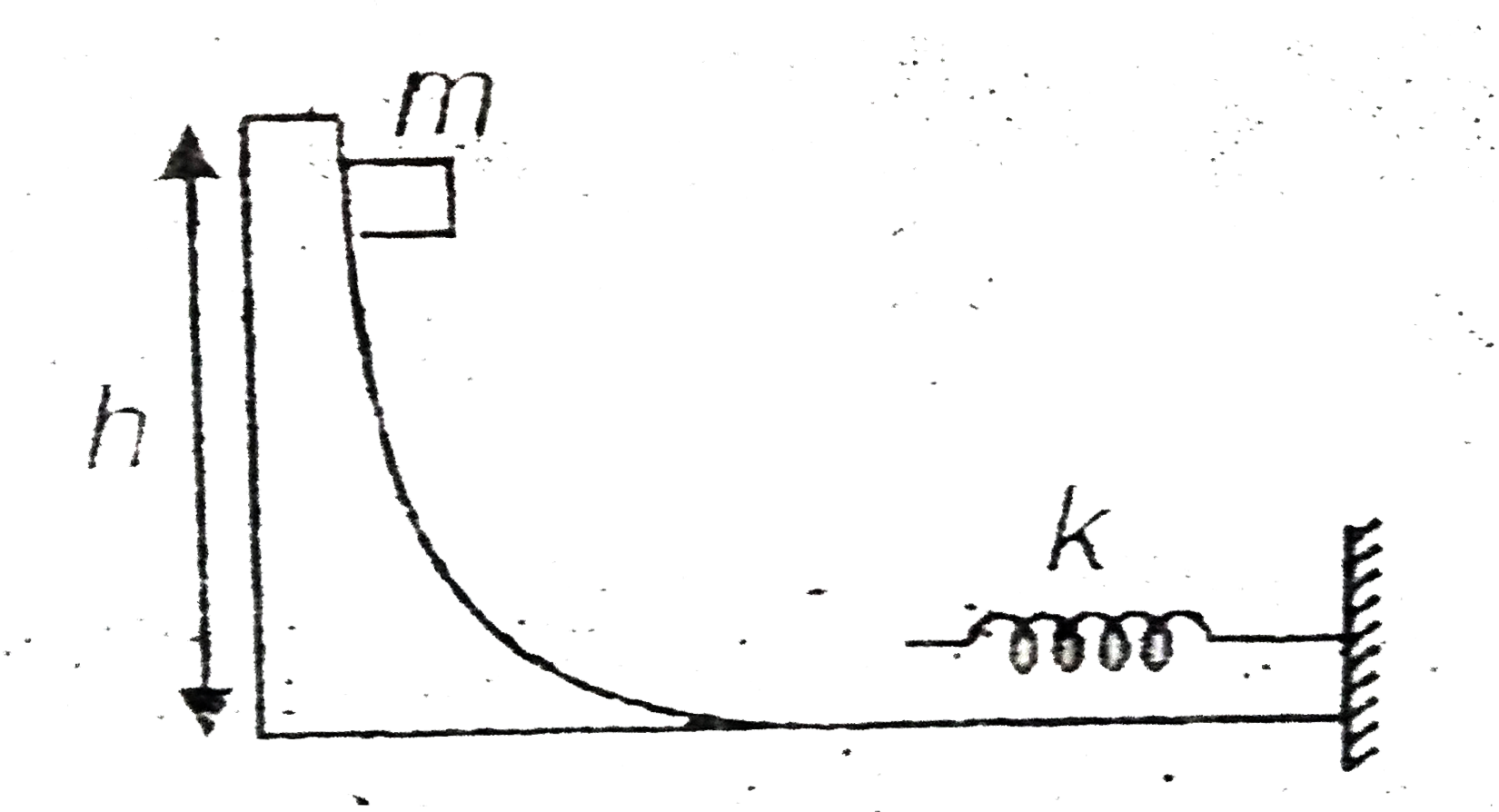
View Solution
Knowledge Check
A car of mass 1000 kg moving with a speed 18kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25×103Nm−1. The maximum compression of the spring is
A1 mB2 mC3 mD4 m
a block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View SolutionA block of mass 2 kg is dropped from a height of 40 cm on a spring whose force-constant 1960Nm−1. The maximum distance through which the spring is compressed by
View SolutionA particle of mass m=1kg is dropped from a height h=40cm on a light horizontal platform fixed to one end of an elastic spring, the other being fixed to a base. The particle collides with the platform and sticks to it. As a result, the spring is compressed by an amount x=10cm. What is the force constant of the spring?
(Take g=10ms−2)
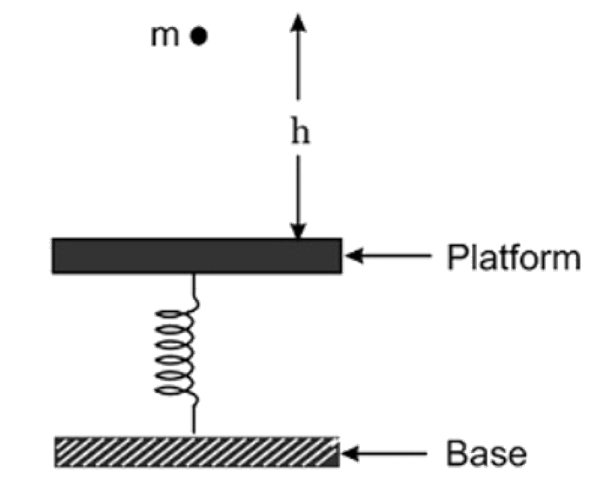
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionA body of mass m falls from a height h on a pan ( of negligible mass ) of spring balance as shwon. The spring is ideal and has a spring contant k. Just after striking the pan, the body sticks with the pan and starts oscillatory motion in vertical direction. The velocity of the body at mean position will be
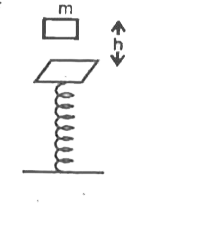
View SolutionA ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View SolutionTwo blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
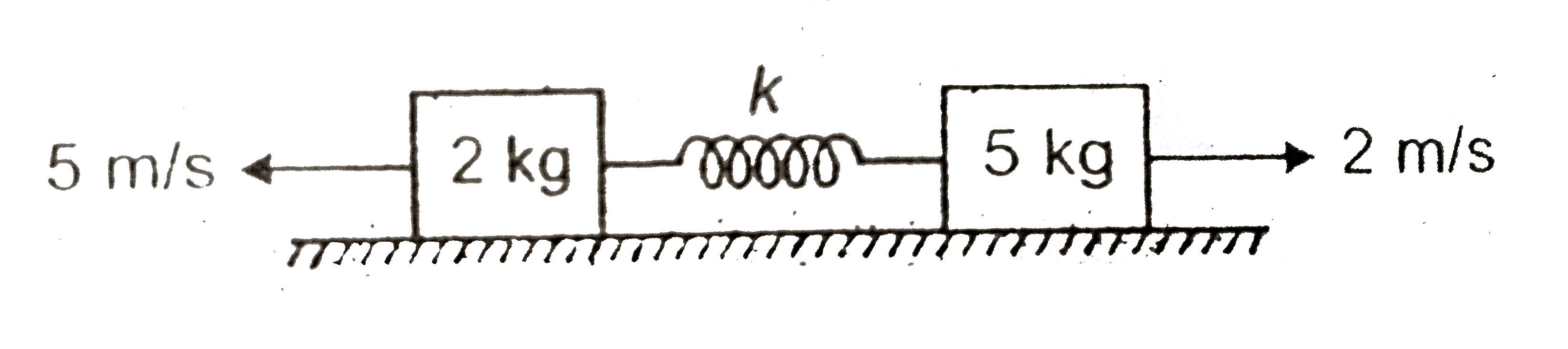
View Solution

