The Ne atom has 10 times the mass of H2 molecule. Which of the following statements is true?
I. At 25∘C both of them have the same kinetic energy.
II. Ten moles of H2 would have the same volume as 1 mole of Ne at same temp. and pressure.
III. One mole of Ne exerts the same pressure as one mole of H2 at STP.
IV. A H2 molecule travels 10 times faster than Ne atom at same temperature.
V. At STP, one litre of Ne has 10 times the density of 1 litre of H2.
II, IV, V
I, III, V
I, II, III
I, II
The correct Answer is:b
To solve the question regarding the Ne atom and H2 molecule, we will analyze each of the statements provided.
Step 1: Understanding the Mass Relationship
The mass of one Ne atom is given to be 10 times that of an H2 molecule.
- Mass of H2 molecule = 2 g/mol
- Mass of Ne atom = 20 g/mol
This confirms that the mass of Ne is indeed 10 times that of H2.
Step 2: Analyzing Statement I
Statement I: At 25°C, both of them have the same kinetic energy.
- The kinetic energy (KE) of a gas is given by the formula:
KE=32RT
- Since R (the gas constant) and T (temperature) are the same for both gases, the kinetic energy will be the same.
- Conclusion: Statement I is True.
Step 3: Analyzing Statement II
Statement II: Ten moles of H2 would have the same volume as 1 mole of Ne at the same temperature and pressure.
- According to the ideal gas law, the volume (V) can be expressed as:
V=nRTP
- For H2 (10 moles):
VH2=10RTP
- For Ne (1 mole):
VNe=1RTP
- Since VH2 is 10 times VNe, they do not have the same volume.
- Conclusion: Statement II is False.
Step 4: Analyzing Statement III
Statement III: One mole of Ne exerts the same pressure as one mole of H2 at STP.
- At STP (Standard Temperature and Pressure), 1 mole of any ideal gas occupies the same volume (22.4 L) and exerts the same pressure (1 atm).
- Therefore, both gases will exert the same pressure.
- Conclusion: Statement III is True.
Step 5: Analyzing Statement IV
Statement IV: An H2 molecule travels 10 times faster than a Ne atom at the same temperature.
- The average speed of gas molecules is given by:
v∝1√M
where M is the molar mass.
- For H2 (M = 2 g/mol) and Ne (M = 20 g/mol):
vH2vNe=√MNeMH2=√202=√10
- Therefore, H2 travels faster than Ne, but not 10 times faster; it travels √10 times faster.
- Conclusion: Statement IV is False.
Step 6: Analyzing Statement V
Statement V: At STP, one liter of Ne has 10 times the density of 1 liter of H2.
- Density (d) is given by:
d=PMRT
- Since pressure (P) and temperature (T) are the same for both gases at STP, the density ratio is directly proportional to their molar masses:
dNedH2=MNeMH2=202=10
- Thus, the density of Ne is indeed 10 times that of H2.
- Conclusion: Statement V is True.
Final Conclusion
The true statements are I, III, and V. The false statements are II and IV.
Summary of True Statements:
- I. True
- II. False
- III. True
- IV. False
- V. True
The mass of one Ne atom is given to be 10 times that of an H2 molecule.
- Mass of H2 molecule = 2 g/mol
- Mass of Ne atom = 20 g/mol
This confirms that the mass of Ne is indeed 10 times that of H2.
Statement I: At 25°C, both of them have the same kinetic energy.
- The kinetic energy (KE) of a gas is given by the formula:
KE=32RT
- Since R (the gas constant) and T (temperature) are the same for both gases, the kinetic energy will be the same.
- Conclusion: Statement I is True.
Statement II: Ten moles of H2 would have the same volume as 1 mole of Ne at the same temperature and pressure.
- According to the ideal gas law, the volume (V) can be expressed as:
V=nRTP
- For H2 (10 moles):
VH2=10RTP
- For Ne (1 mole):
VNe=1RTP
- Since VH2 is 10 times VNe, they do not have the same volume.
- Conclusion: Statement II is False.
Statement III: One mole of Ne exerts the same pressure as one mole of H2 at STP.
- At STP (Standard Temperature and Pressure), 1 mole of any ideal gas occupies the same volume (22.4 L) and exerts the same pressure (1 atm).
- Therefore, both gases will exert the same pressure.
- Conclusion: Statement III is True.
Statement IV: An H2 molecule travels 10 times faster than a Ne atom at the same temperature.
- The average speed of gas molecules is given by:
v∝1√M
where M is the molar mass.
- For H2 (M = 2 g/mol) and Ne (M = 20 g/mol):
vH2vNe=√MNeMH2=√202=√10
- Therefore, H2 travels faster than Ne, but not 10 times faster; it travels √10 times faster.
- Conclusion: Statement IV is False.
Statement V: At STP, one liter of Ne has 10 times the density of 1 liter of H2.
- Density (d) is given by:
d=PMRT
- Since pressure (P) and temperature (T) are the same for both gases at STP, the density ratio is directly proportional to their molar masses:
dNedH2=MNeMH2=202=10
- Thus, the density of Ne is indeed 10 times that of H2.
- Conclusion: Statement V is True.
The true statements are I, III, and V. The false statements are II and IV.
- I. True
- II. False
- III. True
- IV. False
- V. True
Topper's Solved these Questions
- GASEOUS STATEBook:NARENDRA AWASTHI ENGLISHChapter:GASEOUS STATEExercise:Level 2
Explore 30 Videos
- GASEOUS STATEBook:NARENDRA AWASTHI ENGLISHChapter:GASEOUS STATEExercise:Level 3 Passage 1
Explore 4 Videos
- ELECTROCHEMISTRYBook:NARENDRA AWASTHI ENGLISHChapter:ELECTROCHEMISTRYExercise:Subjective problems
Explore 14 Videos
- IONIC EEQUILIBRIUMBook:NARENDRA AWASTHI ENGLISHChapter:IONIC EEQUILIBRIUMExercise:Subjective problems
Explore 1 Video
Similar Questions
Knowledge Check
At what temperature will the total kinetic energy of 0.5 moles of He be the same as the total kinetic energy of 0.6 moles of neon at 300K?
A300 KB360 KC400 KD250 K
Ne, Na+ and F− have the same
View Solution'The number of atoms in 1 mole of hydrogen is twice the number of atoms in 1 mole of helium, at the same temperature and pressure." Why ?
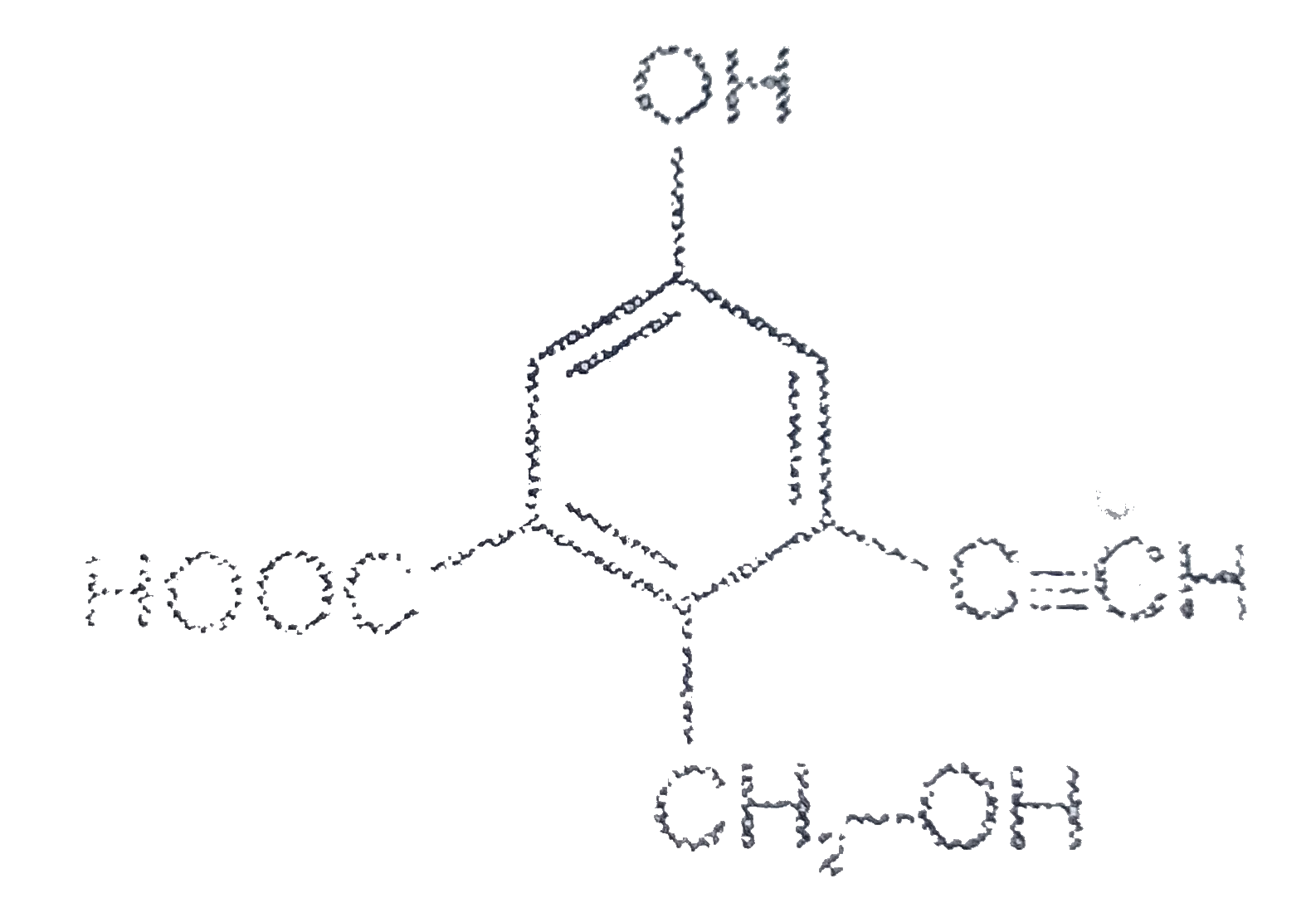
View SolutionNo. of moles of H2 gas evolved when one mole of the following compound reacts with sodium.
View SolutionAt the same temperature and pressure, which of the following will have highest KE per mole
View SolutionWhich of the following ideal gases has higher value of average kinetic energy per mole at the same temperature - N2,CO2,O2 ?
View SolutionAssetion (A): 1 mol H2 and N2 have same volume at same temperature and pressure.
Reason (R ): 1 mol gas at STP occupies 24.4L volume.
View SolutionAt STP, a container has 1 mole of Ar, 2 mole of CO2, 3 moles of O2 and 4 moles of N2. Without changing the total pressure if one mole of O2 is removed, the partial pressure of O2
View Solution

