A conducting loop of area 5.0cm2 is placed in a magnetic field which varies sinusoidally with time as B=B0sinωt where B0 = 0.20 T and ω=300s−1. The normal to the coil makes an angle of 60∘ with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at t=(π900)s and (c) the emf induced at t=(π600)s.
To solve the problem step by step, we will follow the concepts of electromagnetic induction, particularly Faraday's law of induction and the calculation of magnetic flux.
Given Data:
- Area of the coil, A=5.0cm2=5.0×10−4m2
- Magnetic field, B(t)=B0sin(ωt)
- B0=0.20T
- ω=300s−1
- Angle between the normal to the coil and the magnetic field, θ=60∘
Step 1: Calculate the Magnetic Flux
The magnetic flux ΦB through the coil is given by:
ΦB=B⋅A⋅cos(θ)
Substituting B(t):
ΦB=(B0sin(ωt))⋅A⋅cos(θ)
Substituting the values:
ΦB=(0.20sin(300t))⋅(5.0×10−4)⋅cos(60∘)
Since cos(60∘)=12:
ΦB=(0.20sin(300t))⋅(5.0×10−4)⋅12
ΦB=5.0×10−5sin(300t)Wb
Step 2: Calculate the Induced EMF
According to Faraday's law, the induced EMF E is given by:
E=−dΦBdt
Differentiating the magnetic flux:
E=−ddt(5.0×10−5sin(300t))
Using the chain rule:
E=−5.0×10−5⋅300cos(300t)
E=−0.015cos(300t)V
Part (a): Maximum Induced EMF
The maximum induced EMF occurs when cos(300t)=1:
Emax=0.015V
Part (b): Induced EMF at t=π900s
Substituting t=π900:
E=−0.015cos(300⋅π900)
Calculating:
300⋅π900=π3
Thus:
E=−0.015cos(π3)=−0.015⋅12=−0.0075V
The induced EMF is:
E=7.5×10−3V
Part (c): Induced EMF at t=π600s
Substituting t=π600:
E=−0.015cos(300⋅π600)
Calculating:
300⋅π600=π2
Thus:
E=−0.015cos(π2)=−0.015⋅0=0V
Final Answers:
(a) Maximum EMF: 0.015V
(b) EMF at t=π900s: 7.5×10−3V
(c) EMF at t=π600s: 0V
- Area of the coil, A=5.0cm2=5.0×10−4m2
- Magnetic field, B(t)=B0sin(ωt)
- B0=0.20T
- ω=300s−1
- Angle between the normal to the coil and the magnetic field, θ=60∘
The magnetic flux ΦB through the coil is given by:
ΦB=B⋅A⋅cos(θ)
Substituting B(t):
ΦB=(B0sin(ωt))⋅A⋅cos(θ)
Substituting the values:
ΦB=(0.20sin(300t))⋅(5.0×10−4)⋅cos(60∘)
Since cos(60∘)=12:
ΦB=(0.20sin(300t))⋅(5.0×10−4)⋅12
ΦB=5.0×10−5sin(300t)Wb
According to Faraday's law, the induced EMF E is given by:
E=−dΦBdt
Differentiating the magnetic flux:
E=−ddt(5.0×10−5sin(300t))
Using the chain rule:
E=−5.0×10−5⋅300cos(300t)
E=−0.015cos(300t)V
The maximum induced EMF occurs when cos(300t)=1:
Emax=0.015V
Substituting t=π900:
E=−0.015cos(300⋅π900)
Calculating:
300⋅π900=π3
Thus:
E=−0.015cos(π3)=−0.015⋅12=−0.0075V
The induced EMF is:
E=7.5×10−3V
Substituting t=π600:
E=−0.015cos(300⋅π600)
Calculating:
300⋅π600=π2
Thus:
E=−0.015cos(π2)=−0.015⋅0=0V
(a) Maximum EMF: 0.015V
(b) EMF at t=π900s: 7.5×10−3V
(c) EMF at t=π600s: 0V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
Similar Questions
A conducting looop of area 5.0cm2 is placed in a magnetic field which varies sinusoidally with time as B=0.2sin300t . The normal to the coil makes an angle of 60∘ with the field. The emf induced at t=(π/900)s
View SolutionA coil of 100 turns and area 5 square centimetre is placed in a magnetic field B = 0.2 T . The normal to the plane of the coil makes an angle of 60∘ with the direction of the magnetic field. The magnetic flux linked with the coil is
View Solution
Knowledge Check
A conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
Aπ2r4B402τRBπ2r4B202τRCπ2r4B20RτDπ2r4B20τR
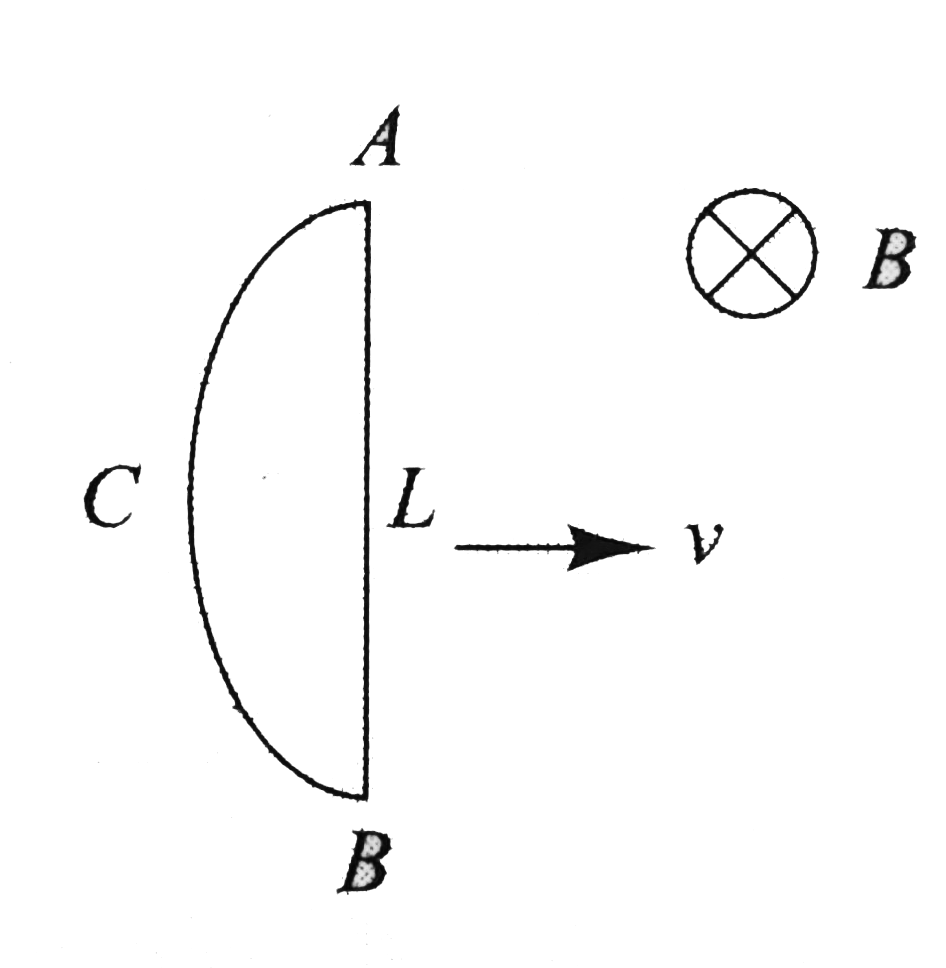
Shows a closed coil ABCL moving in a uniform magnetic field B with a velocity v.
Find
(a) emf induced in the coil.
(b) emf induced in curve part ACB and straight AB
View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
View SolutionA coil having an area A0 is placed in a magnetic field which changes from B0 to 4B0 in time interval t. The emf induced in the coil will be
View SolutionA varying current ina coils changes from 10 A to zero in 0.5s .If the average emf induced in the coils is 220 V , the self- inductance of the coils is
View SolutionA metallic loop is placed in a nonuniform magnetic field. Will an emf be induced in the loop?
View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is

View SolutionA square conductind loop, 20.0cm on a side placed in the same magnetic field as shown in Fig. 3.195, center of the magnetic field region, where dB/dt=0.035Ts−1.

he direction of induced electric field at points a, b and c:
View Solution
