A coducting circular loop of area 1mm2 is placed coplanarly with a long, straight wire at a distance of 20 cm from if. The straight wire carries an electric current which changes from 10A to zero is 0.1 s. Find the average emf induced in the loop in 0.1 s.
To find the average emf induced in a conducting circular loop due to a changing current in a nearby straight wire, we will follow these steps:
Step 1: Understand the Problem
We have a conducting circular loop with an area of 1mm2 placed at a distance of 20cm from a straight wire carrying a current that changes from 10A to 0A in 0.1s. We need to calculate the average emf induced in the loop during this time.
Step 2: Convert Units
Convert the area of the loop from mm2 to m2:
1mm2=1×10−6m2
Convert the distance from cm to m:
20cm=0.2m
Step 3: Calculate the Change in Magnetic Field
The magnetic field B at a distance r from a long straight wire carrying a current I is given by:
B=μ0I2πr
where μ0=4π×10−7T m/A.
Initially (when I=10A):
B1=4π×10−7×102π×0.2=4×10−60.4=1×10−5T
Finally (when I=0A):
B2=0T
Step 4: Calculate the Change in Magnetic Flux
The magnetic flux Φ through the loop is given by:
Φ=B⋅A
where A is the area of the loop. The change in magnetic flux ΔΦ is:
ΔΦ=Φ2−Φ1=B2⋅A−B1⋅A=0−(1×10−5⋅1×10−6)=−1×10−11Wb
Step 5: Calculate the Average Induced EMF
The average induced emf (E) can be calculated using Faraday's law of electromagnetic induction:
E=−ΔΦΔt
Substituting the values:
E=−−1×10−110.1=1×10−10V
Final Answer
The average emf induced in the loop is:
E=1×10−10V
---
We have a conducting circular loop with an area of 1mm2 placed at a distance of 20cm from a straight wire carrying a current that changes from 10A to 0A in 0.1s. We need to calculate the average emf induced in the loop during this time.
Convert the area of the loop from mm2 to m2:
1mm2=1×10−6m2
Convert the distance from cm to m:
20cm=0.2m
The magnetic field B at a distance r from a long straight wire carrying a current I is given by:
B=μ0I2πr
where μ0=4π×10−7T m/A.
B1=4π×10−7×102π×0.2=4×10−60.4=1×10−5T
B2=0T
The magnetic flux Φ through the loop is given by:
Φ=B⋅A
where A is the area of the loop. The change in magnetic flux ΔΦ is:
ΔΦ=Φ2−Φ1=B2⋅A−B1⋅A=0−(1×10−5⋅1×10−6)=−1×10−11Wb
The average induced emf (E) can be calculated using Faraday's law of electromagnetic induction:
E=−ΔΦΔt
Substituting the values:
E=−−1×10−110.1=1×10−10V
The average emf induced in the loop is:
E=1×10−10V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
Similar Questions
A conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

View SolutionAn electric current passes through a long straight copper wire. At a distance of 5 cm from the straight wire, the magnetic field is B. What is the magnetic field at a distance of 20 cm from the wire ?
View SolutionA current I=3.36(1+2t)×10−2 A increase at a steady state in a long staight wire. A small circular loop of radius 10−3 m has its plane parallel to the wire and is placed at a distance of 1 m from the wire. The resistance of loop is 8.4×10−4(Ω). Find the approximate value of induced current in the loop.
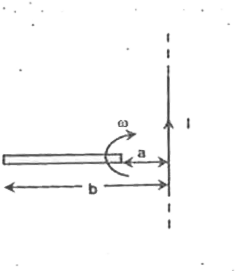
View SolutionA copper rod moves with a constant angular velocity ω about a long straight wire carrying a current I. If the ends of the rod from the wire are at distances a and b, then the e.m.f induced in the rod is
View SolutionA long straight wire is carrying a current of 25 A. A squre loop of side length 10 cm carrying a current of 15 A, is placed 2 cm from the wire as shown in figure. The force on the loop is

View SolutionShow a conduction loop placed near a long, straight wire carrying current i as shown. If the current increases continuously, find the direction of the induced current in the loop.

View SolutionFigure shows a conducting loop placed near a long straight wire carrying a current i as shown, if the current increases continuously, find the direction of the induced current in the loop.

View SolutionA conducintg circular loop having a redius of 5.0cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced In the loop during this time.
View SolutionA long straight current carrying wire passes normally through the centre of circular loop. If the current through the wire increases, will there be an induced emf in the loop ? Justify.
View SolutionA square loop of wire with side length 10 cm is placed at angle of 45∘ with a magnetic field that changes uniformly from 0.1 T to zero in 0.7s. The induced current in the loop (its resistance is 1Ω) is
View Solution
