A square loop of wire with side length 10 cm is placed at angle of 45∘ with a magnetic field that changes uniformly from 0.1 T to zero in 0.7s. The induced current in the loop (its resistance is 1Ω) is
1.0 mA
2.5 mA
3.5 mA
4.0 mA
The correct Answer is:A
To solve the problem step by step, we will follow the principles of electromagnetic induction and use the relevant formulas.
Step 1: Identify the given parameters
- Side length of the square loop, L=10cm=0.1m
- Angle with the magnetic field, θ=45∘
- Initial magnetic field, Bi=0.1T
- Final magnetic field, Bf=0T
- Time taken for the change, t=0.7s
- Resistance of the loop, R=1Ω
Step 2: Calculate the area of the square loop
The area A of the square loop is given by:
A=L2=(0.1m)2=0.01m2
Step 3: Calculate the change in magnetic flux
The magnetic flux Φ through the loop is given by:
Φ=B⋅A⋅cos(θ)
- Initial flux Φi:
Φi=Bi⋅A⋅cos(45∘)=0.1⋅0.01⋅1√2=0.001√2Wb
- Final flux Φf:
Φf=Bf⋅A⋅cos(45∘)=0⋅0.01⋅1√2=0Wb
Step 4: Calculate the change in flux
The change in flux ΔΦ is:
ΔΦ=Φf−Φi=0−0.001√2=−0.001√2Wb
Step 5: Calculate the induced EMF
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−ΔΦt=−−0.001√20.7
E=0.0010.7√2V
Step 6: Calculate the induced current
Using Ohm's law, the induced current I can be calculated as:
I=ER=0.0010.7√21
I=0.0010.7√2A
Step 7: Numerical calculation
Calculating the numerical value:
√2≈1.414
I≈0.0010.7×1.414≈0.0010.9898≈0.00101A≈1.01mA
Final Answer
The induced current in the loop is approximately 1.01mA.
---
- Side length of the square loop, L=10cm=0.1m
- Angle with the magnetic field, θ=45∘
- Initial magnetic field, Bi=0.1T
- Final magnetic field, Bf=0T
- Time taken for the change, t=0.7s
- Resistance of the loop, R=1Ω
The area A of the square loop is given by:
A=L2=(0.1m)2=0.01m2
The magnetic flux Φ through the loop is given by:
Φ=B⋅A⋅cos(θ)
- Initial flux Φi:
Φi=Bi⋅A⋅cos(45∘)=0.1⋅0.01⋅1√2=0.001√2Wb
- Final flux Φf:
Φf=Bf⋅A⋅cos(45∘)=0⋅0.01⋅1√2=0Wb
The change in flux ΔΦ is:
ΔΦ=Φf−Φi=0−0.001√2=−0.001√2Wb
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−ΔΦt=−−0.001√20.7
E=0.0010.7√2V
Using Ohm's law, the induced current I can be calculated as:
I=ER=0.0010.7√21
I=0.0010.7√2A
Calculating the numerical value:
√2≈1.414
I≈0.0010.7×1.414≈0.0010.9898≈0.00101A≈1.01mA
The induced current in the loop is approximately 1.01mA.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A square wire loop of side 30cm & wire cross section having diameter 4mm is placed perpendicular to a magnetic field changing at the rate 0.2 T/s. Final induced current in the wire loop.
(Given: Resistivity of wire material is (1.23×10−8ohmm)
View SolutionA uniform magnetic field B exist in a direction perpedicuar to the plane of a square loop made of a metal wire. The wire has diameter of 4 mm and a total length of 30 cm . The magnetic field changes with time at a steady rate dB/dt = 0.032 Ts−1 . The induced current in the loop is close to (Resistivity of the metal wire is 1.23×10−8Ωm)
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA circular loop of radius 1m is placed in a varying magnetic field given as B=6t Tesla, where t is time in sec.
(a)Find the emf induced in the coil if the plane of the coil is perpendicular to the magnetic field.
(b) Find the electric field in the tangential directin, induced due to the changing magnetic field.
(c)Find the current in the loop if its resistance is 1Ω/m.
View SolutionA coil having 500 square loops each of side 10cm is placed normal to a magnetic flux which increase at the rate of 1.0teslasecond. The induced r.m.f. in volts is
View SolutionA square conductind loop, 20.0cm on a side placed in the same magnetic field as shown in Fig. 3.195, center of the magnetic field region, where dB/dt=0.035Ts−1.

The current induced in the loop if its resistance is 2.00Ω is
View SolutionA circular loop is placed in magnetic field B=2t. Find the direction of induced current produced in the loop.

View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)
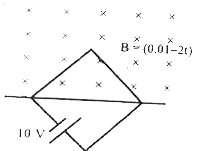
View SolutionA square loop of side 1 m is placed in a perpendicular magnetic field. Half of the area of the loop lies inside the magnetic field . A battery of emf 10 V and negligible intermal resistance is connected in the loop . The magnetic field changes with time according to the relation B= (0.01 -2t) tesla . The resultant emf of the circuit is
View SolutionA square loop of side 6cm carries a current of 30A. Calculate the magnitude of magnetic field B at a point P lying on the axis of the loop and a distance√7 cm from centre of the loop.
View Solution
