An inductor-resistance -battery circuit is switched on at t = 0. find the emf of the battery in one time constant .
To solve the problem of finding the EMF of the battery in an inductor-resistor circuit at one time constant, we can follow these steps:
1. Understand the Circuit Components:
- We have a circuit consisting of a battery with EMF V, an inductor with inductance L, and a resistor with resistance R. The switch is closed at t=0.
2. Current in the Circuit:
- The current I(t) in the circuit as a function of time after the switch is closed is given by:
I(t)=I0(1−e−tτ)
- Here, τ=LR is the time constant and I0 is the maximum current given by I0=VR.
3. Differentiate the Current:
- To find the induced EMF, we need to calculate the rate of change of current dIdt:
dIdt=ddt(I0(1−e−tτ))
- Differentiating gives:
dIdt=I0⋅1τe−tτ
4. Calculate the EMF:
- The induced EMF E in the inductor can be calculated using:
E=LdIdt
- Substituting the expression for dIdt:
E=L⋅I0⋅1τe−tτ
5. Evaluate at One Time Constant:
- We need to evaluate the EMF at t=τ:
E=L⋅I0⋅1τe−1
- Since I0=VR:
E=L⋅VR⋅1τ⋅e−1
6. Substitute τ:
- Recall that τ=LR:
E=L⋅VR⋅RL⋅e−1
- The L and R cancel out:
E=V⋅e−1
Final Answer:
The EMF of the battery at one time constant is:
E=Ve
- We have a circuit consisting of a battery with EMF V, an inductor with inductance L, and a resistor with resistance R. The switch is closed at t=0.
- The current I(t) in the circuit as a function of time after the switch is closed is given by:
I(t)=I0(1−e−tτ)
- Here, τ=LR is the time constant and I0 is the maximum current given by I0=VR.
- To find the induced EMF, we need to calculate the rate of change of current dIdt:
dIdt=ddt(I0(1−e−tτ))
- Differentiating gives:
dIdt=I0⋅1τe−tτ
- The induced EMF E in the inductor can be calculated using:
E=LdIdt
- Substituting the expression for dIdt:
E=L⋅I0⋅1τe−tτ
- We need to evaluate the EMF at t=τ:
E=L⋅I0⋅1τe−1
- Since I0=VR:
E=L⋅VR⋅1τ⋅e−1
- Recall that τ=LR:
E=L⋅VR⋅RL⋅e−1
- The L and R cancel out:
E=V⋅e−1
The EMF of the battery at one time constant is:
E=Ve
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:HC VERMA ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Objective 1
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:HC VERMA ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Objective 2
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:HC VERMA ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Questions for short answer
Explore 9 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:Objective 2
Explore 7 Videos
- ELECTROMAGNETIC WAVESBook:HC VERMA ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Exercise
Explore 8 Videos
Similar Questions
Consider the circuit shown. Switch is closed at t=0. Find the current through the battery as a function of time. Initially capacitor was uncharged.
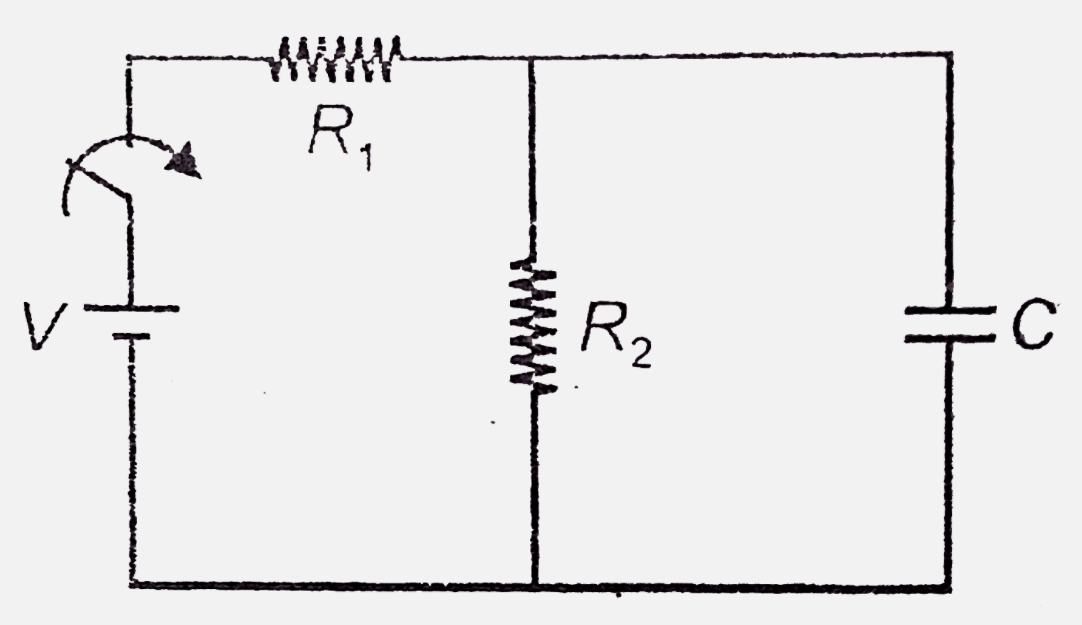
View SolutionIn the circuit shown in figure switch S is closed at time t=0. The charge which passes through the battery in one time constant is

View SolutionThe figure shows three circuits with identica batteries, inductors and resistances. Rank the circuits according to the currents through the battery just after the switch is closed, greatest fire
View SolutionThe figure below shows a battery of emf ε connected to an inductor L and resistance R in series. If the switch is closed at t=0, then the total charge that flows from the battery in time constant of the circuit is
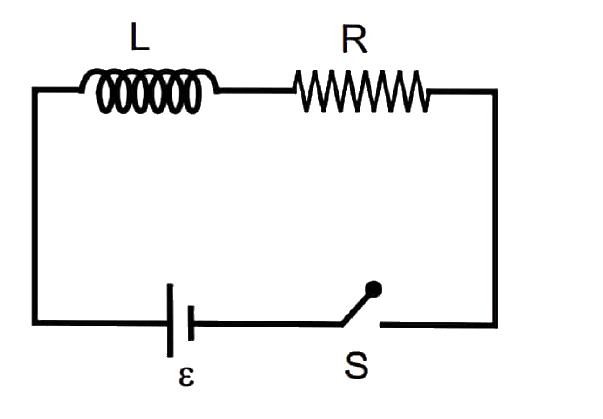
View SolutionThe switch shown in figure is closed at t=0 find the charge throuh battery till time t=LR
_2019_CBT8_E01_016_Q01.png)
View SolutionThe switch shown in figure is closed at t=0 find the charge throuh battery till time t=LR
_2019_CBT8_E01_016_Q01.png)
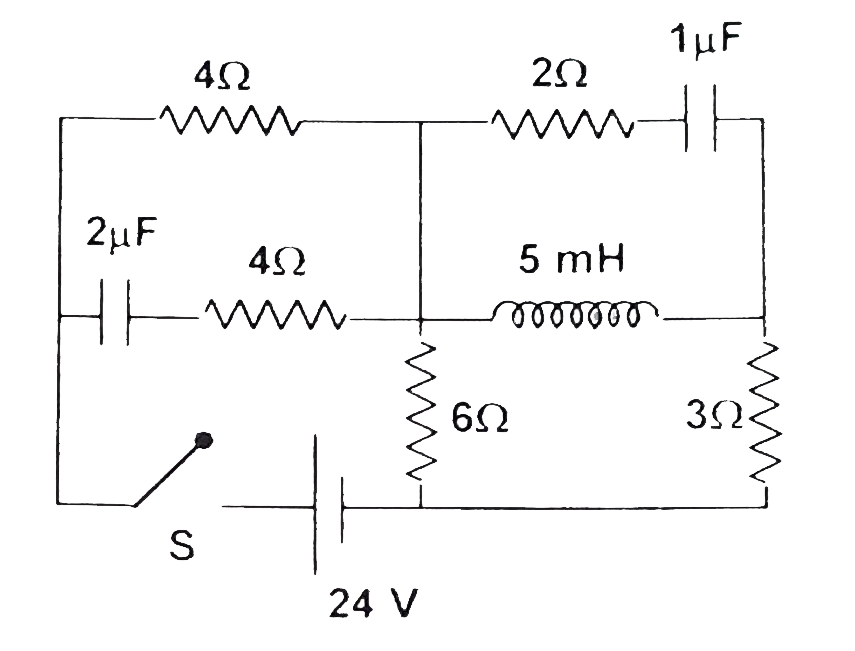
View SolutionIn the circuit shown, the switch 'S' is closed at t=0. Then the current through the battery steady state reached is
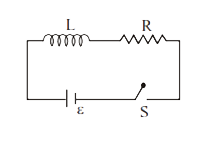
View SolutionAs shown in the figure, a battery of emf ε is connected to an inductor L and resistance R in series. The switch is closed at t=0 . The total charge that flows from the battery, between t=te and t=2te (te is the time constant of the circuit) is:
View SolutionThe figure shows three circuits with identical batteries, inductors and resistance . Rank the circuits in decreasing order, according to the current through the battery just after the switch is closed
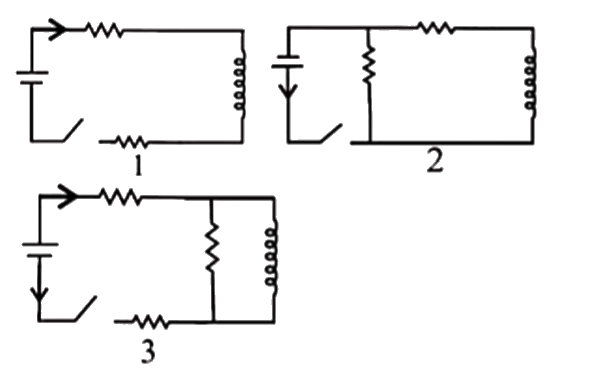
View Solution As shown in the figur a battery of emf ∈ is conneced to an inductor L and resistance R in series . The swith is closed at t =0 . The total charge that flows form the battery between t 0 and t=tc (tc is the time constant of the circuit )is :
As shown in the figur a battery of emf ∈ is conneced to an inductor L and resistance R in series . The swith is closed at t =0 . The total charge that flows form the battery between t 0 and t=tc (tc is the time constant of the circuit )is :
View Solution