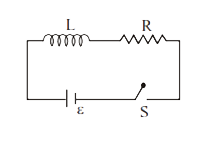
As shown in the figure, a battery of emf ε is connected to an inductor L and resistance R in series. The switch is closed at t=0 . The total charge that flows from the battery, between t=te and t=2te (te is the time constant of the circuit) is:
εLR2(1−1e)
εLR2(1+1e2−1e)
εLR2(1+2e2−1e)
εLeR2
The correct Answer is:B
i=i0(1−eRt/L)=i0(1−e−t/tc)
q=∫2tctci dt =∫2tctcεR(1−e−t/tc)dt=εLR2(1+1e2−1e)
Topper's Solved these Questions
Similar Questions
As shown in the figure, a battery of emf is connected to an inductor L and resistance R in series. The switch is closed at . The total charge that flows from the battery, between t=te and t=2te (te is the time constant of the circuit) is:

View Solution As shown in the figur a battery of emf ∈ is conneced to an inductor L and resistance R in series . The swith is closed at t =0 . The total charge that flows form the battery between t 0 and t=tc (tc is the time constant of the circuit )is :
As shown in the figur a battery of emf ∈ is conneced to an inductor L and resistance R in series . The swith is closed at t =0 . The total charge that flows form the battery between t 0 and t=tc (tc is the time constant of the circuit )is :
View SolutionThe figure below shows a battery of emf ε connected to an inductor L and resistance R in series. If the switch is closed at t=0, then the total charge that flows from the battery in time constant of the circuit is
View SolutionTwo inductors are connected in parallel and switch S is closed at t=0

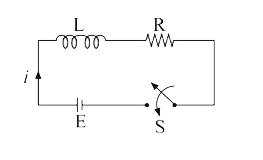
View SolutionConsider the LR circuit shown in the figure. If the switch S is closed at t = 0 then the amount of charge that passes through the battery between t=0 and t=LR is
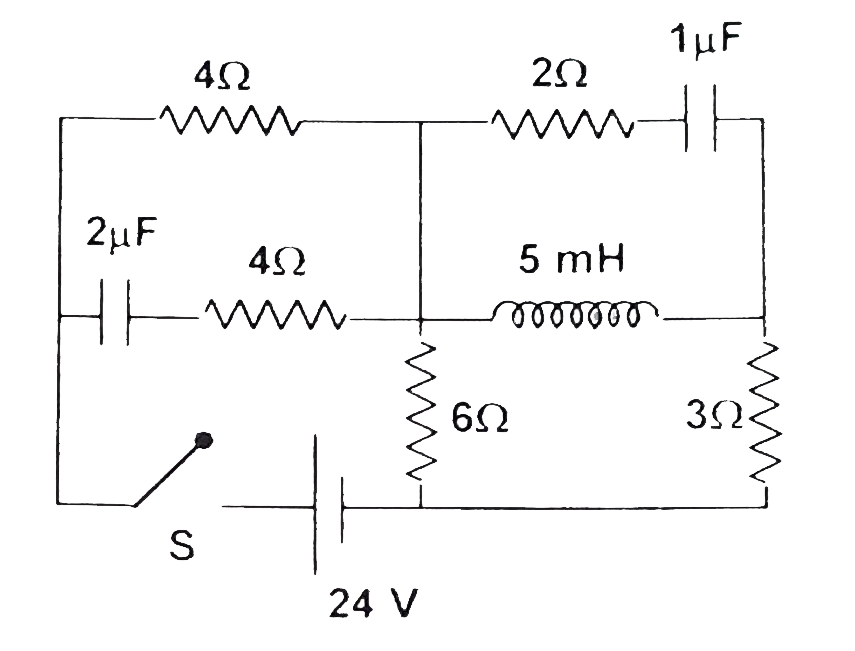
View SolutionIn the circuit shown, the switch 'S' is closed at t=0. Then the current through the battery steady state reached is
View SolutionThe switch shown in figure is closed at t=0 find the charge throuh battery till time t=LR
_2019_CBT8_E01_016_Q01.png)
View SolutionThe switch shown in figure is closed at t=0 find the charge throuh battery till time t=LR
_2019_CBT8_E01_016_Q01.png)
View SolutionCalculate the ratio of current flowing through the battery at t = 0 and t=∞ (t = 0 is the time of closing of the switch)
View SolutionAn uncharged capacitor of capacitance C is connected with a battery of EMF V and a resistance R. The switch is closed at t=0. The time instant at which the current in the circuit is V4R is t=
View Solution
