Suppose ana attractive nuclear force acts between two protons which may be written as F=Ce−kr/r2, (a) Write down the dimensional formulae and appporpriate SI units of C and k. (b) Suppose that k=1fermi−1 and that the repulsive electreic force between the protons is just blanced by the attractive nuclear force when the separation is 5 fermi. Find the value of c.
Let's solve the question step by step.
Part (a): Finding the Dimensional Formulae and SI Units of C and k
1. Understanding the Force Equation:
The attractive nuclear force between two protons is given by:
F=Ce−krr2
Here, F is the force, C is a constant, k is a constant related to the range of the force, and r is the separation distance.
2. Dimensional Formula for Force:
The dimensional formula for force F is:
(F)=M1L1T−2
3. Dimensional Formula for C:
We can express the right-hand side of the equation:
(F)=(C)(r2)
Rearranging gives:
(C)=(F)⋅(r2)
Substituting the dimensions:
(C)=(M1L1T−2)⋅(L2)=M1L3T−2
Therefore, the dimensional formula for C is:
(C)=M1L3T−2
4. SI Unit of C:
The SI unit of force is Newton (N), and the SI unit of length is meter (m). Thus, the SI unit for C is:
SI unit of C=N⋅m2=Newton meter square (N m2)
5. Dimensional Formula for k:
Since e−kr is dimensionless, the product kr must also be dimensionless. Thus, we have:
(k)⋅(r)=1
Therefore, the dimensional formula for k is:
(k)=(L)−1=M0L−1T0
6. SI Unit of k:
The SI unit of k is the inverse of length, which is:
SI unit of k=m−1 (meter inverse)
Part (b): Finding the Value of C
1. Given Values:
- Separation r=5 Fermi=5×10−15 m
- k=1 Fermi−1=1×1015 m−1
- The electrostatic force Fe balances the nuclear force Fn.
2. Electrostatic Force:
The electrostatic force between two protons is given by Coulomb's law:
Fe=keq1q2r2
Where ke=9×109 N m2/C2 and q1=q2=e=1.6×10−19 C.
3. Setting Forces Equal:
Since Fe=Fn:
kee2r2=Ce−krr2
Canceling r2 gives:
kee2=Ce−kr
4. Substituting Known Values:
Substitute ke, e, k, and r:
9×109×(1.6×10−19)2=Ce−1×1015×5×10−15
Simplifying the exponent:
e−5≈0.00674
5. Calculating C:
Rearranging gives:
C=9×109×(1.6×10−19)2e−5
Calculating the left side:
C=9×109×2.56×10−380.00674≈3.4×10−26 N m2
Final Answers:
- (a) Dimensional formula for C: M1L3T−2; SI unit: Newton meter square (N m²).
- (a) Dimensional formula for k: M0L−1T0; SI unit: meter inverse (m⁻¹).
- (b) Value of C: 3.4×10−26 N m2.
The attractive nuclear force between two protons is given by:
F=Ce−krr2
Here, F is the force, C is a constant, k is a constant related to the range of the force, and r is the separation distance.
The dimensional formula for force F is:
(F)=M1L1T−2
We can express the right-hand side of the equation:
(F)=(C)(r2)
Rearranging gives:
(C)=(F)⋅(r2)
Substituting the dimensions:
(C)=(M1L1T−2)⋅(L2)=M1L3T−2
Therefore, the dimensional formula for C is:
(C)=M1L3T−2
The SI unit of force is Newton (N), and the SI unit of length is meter (m). Thus, the SI unit for C is:
SI unit of C=N⋅m2=Newton meter square (N m2)
Since e−kr is dimensionless, the product kr must also be dimensionless. Thus, we have:
(k)⋅(r)=1
Therefore, the dimensional formula for k is:
(k)=(L)−1=M0L−1T0
The SI unit of k is the inverse of length, which is:
SI unit of k=m−1 (meter inverse)
- Separation r=5 Fermi=5×10−15 m
- k=1 Fermi−1=1×1015 m−1
- The electrostatic force Fe balances the nuclear force Fn.
The electrostatic force between two protons is given by Coulomb's law:
Fe=keq1q2r2
Where ke=9×109 N m2/C2 and q1=q2=e=1.6×10−19 C.
Since Fe=Fn:
kee2r2=Ce−krr2
Canceling r2 gives:
kee2=Ce−kr
Substitute ke, e, k, and r:
9×109×(1.6×10−19)2=Ce−1×1015×5×10−15
Simplifying the exponent:
e−5≈0.00674
Rearranging gives:
C=9×109×(1.6×10−19)2e−5
Calculating the left side:
C=9×109×2.56×10−380.00674≈3.4×10−26 N m2
- (a) Dimensional formula for C: M1L3T−2; SI unit: Newton meter square (N m²).
- (a) Dimensional formula for k: M0L−1T0; SI unit: meter inverse (m⁻¹).
- (b) Value of C: 3.4×10−26 N m2.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:question for short answer
Explore 14 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:Objective 1
Explore 9 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:worked out Examples
Explore 19 Videos
- ELECTRIC CURRENT THROUGH GASESBook:HC VERMA ENGLISHChapter:ELECTRIC CURRENT THROUGH GASESExercise:Short answer
Explore 6 Videos
- ELECTROMAGNETIC INDUCTIONBook:HC VERMA ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Questions for short answer
Explore 9 Videos
Similar Questions
Find the electric force between two protons separted by a distance of 1 fermi (1fermi=1015m). The protons in a nucleus remain at a separaton of this order.
View SolutionSuppose the magnitude of Nuclear force between two protons varies with the distance between them as shown in figure. Estimate the ratio Nuclear force/Coulomb force for a. x=8 fm b. x=4 fm, c. x=2 fm and d. x=1 fm (1fm=10−15m).
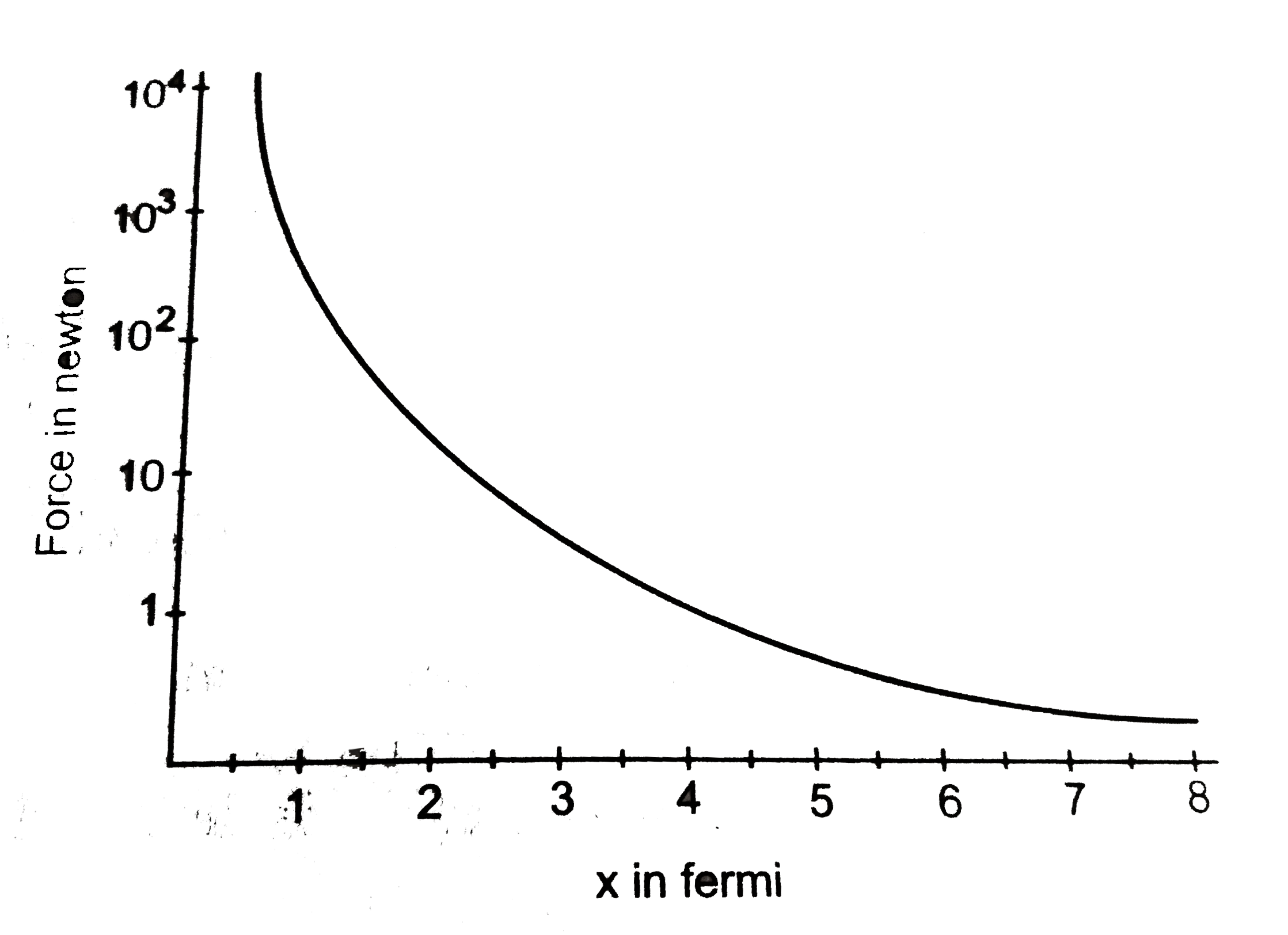
View Solution
Knowledge Check
The potential energy U of two atoms of a diatomic molecule as a function of distance r between the atoms as shown in the given figure.
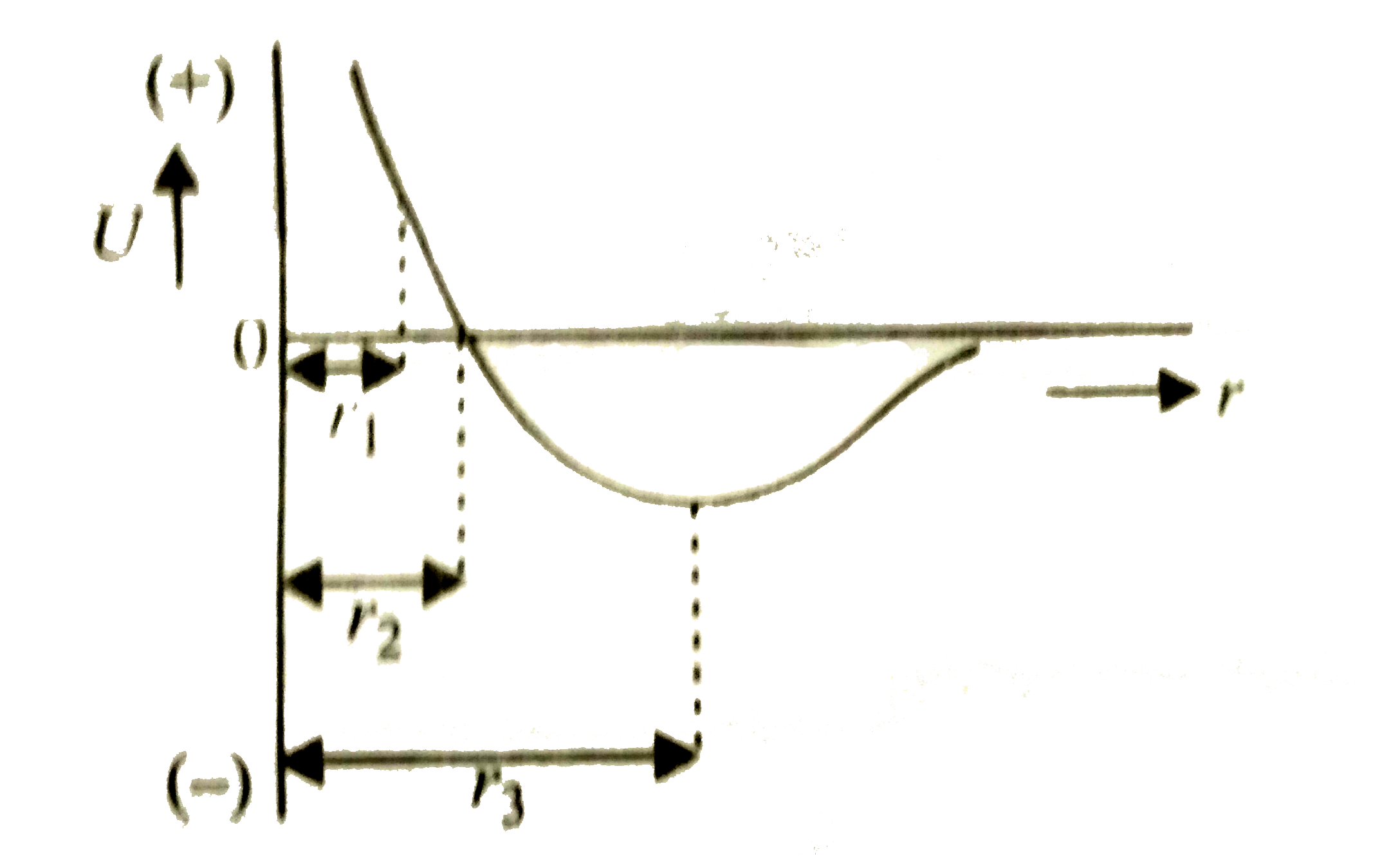
Read the following statement carefully.
1. The equilibrium separation distance between the atoms is equal to r2.
2. At r=r1, the force between the atom is repulsive.
. Forr>r2, the force between the atoms is attractive
Which of the above statements is true ?A1 onlyBÂ 2 onlyCÂ 3 onlyD2 and 3
The electrostatic force between two charges Q1andQ2 at separation r is given by F=K.Q1Q2r2 The constant K
View SolutionThe amount of charge passed in time t through a cross-section of a wire is
Q(t)=At2+Bt+C.
(a)Write the dimensional formulae for A,B and C.
(b) If the numerical values of A,B,and C are 5,3 and 1 respectively in SI units,find the value of the current at t=5 s.
View SolutionCoulomb's law for electrostatic force between two point charges and Newton's law for gravitational force between two stationary point masses, both have inverse square dependence on the distance between the charges/masees (a) compare the strength of these forces by determining the ratio of their maagnitudes (i) for an electron and as proton (ii) for two protons (b) estimate the accelerations for election and proton due to electrical force of their mutal attraction when they are 1 A apart.
View Solution(a) Two protons are placed at some separation in vacuum. Find the ratio of electric and gravitational force acting between them.
(b) Two point charges are placed at separation 3m in vacuum. What can be the minimum force between them.
(c ) A charge Q is to be divided on two objects. What should be the value of the charges in the objects so that the force between them is maximum ?
(d) Two insulating small spheres are rubbed against each other and placed 1.6cm apart. If they attract each other with a force of 0.9N, how many electrons were transferred from one sphere to the other during rubbing ?
View SolutionConsider a sphere of radius R with harge density distributed as p(r)=kr fro r≤R=0 for r>R.
(a). Find the electric field as all points r.
(b) Suppose the total charge on the sphere is 2e where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero. Assume that the introduction of the proton does not alter the negative charge distribution.
View SolutionA capacitance balance is shown in the figure. The balance has a block pulley system attached on one side and a capacitor that has a variable gap width on the other side. Assume upper plate of the capacitor has negligible mass. When the separation between the plate is 1√5 meter, the attractive force between the plates balances the pulley block system. Then find value of V0 in volts (EMF of battery). (Take area of the plate =203ε0m2)

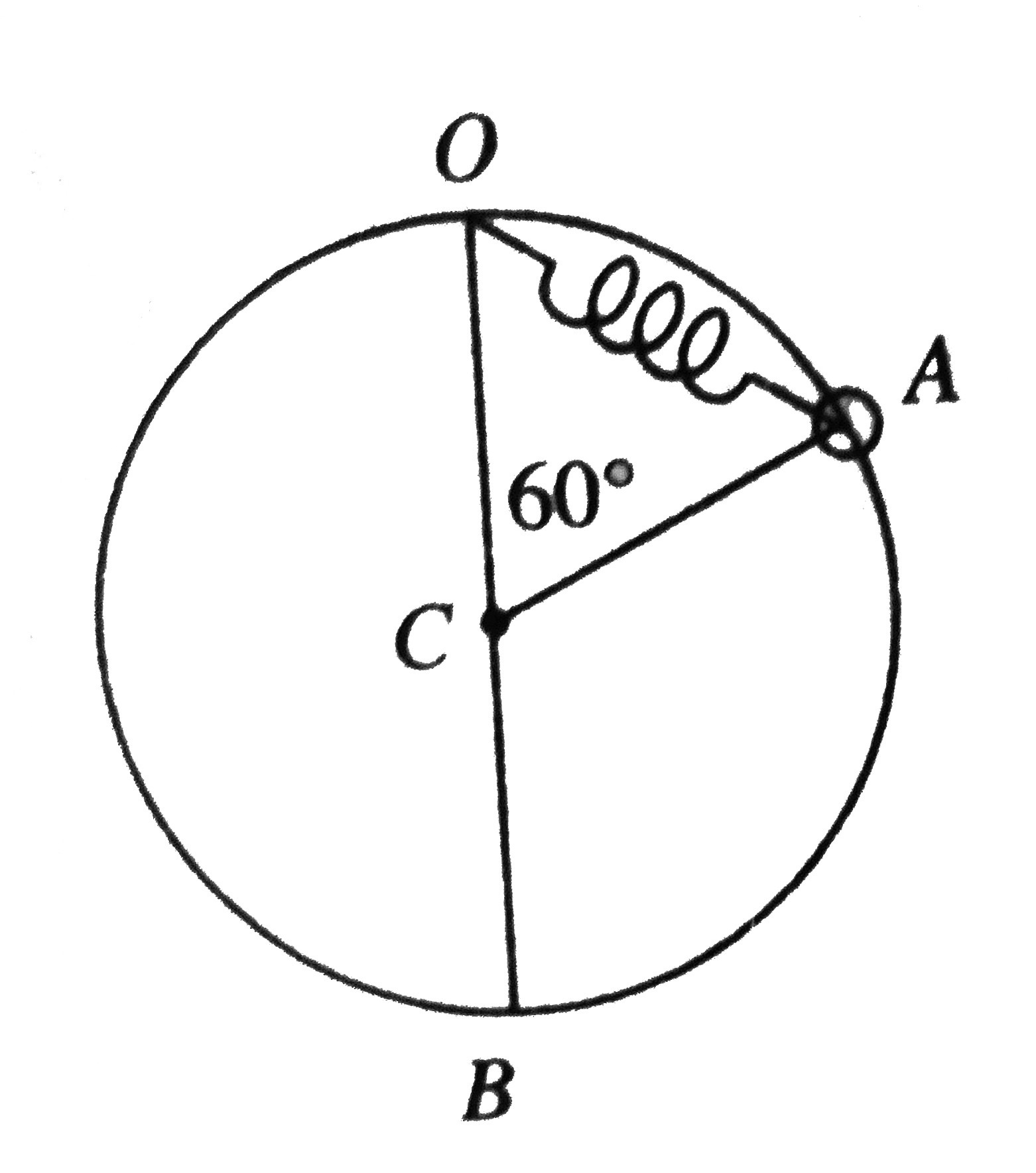
View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
View Solution

