A hot body placed in a surrounding of temperature θ0 obeys Newton's law of cooling dθdt=−k(θ−θ0) . Its temperature at t=0 is θ1 the specific heat capacity of the body is s and its mass is m. Find
(a) the maximum heat that the body can lose and
(b) the time starting from t=0 in which it will lose 90% of this maximum heat.
The correct Answer is:A, B
Given :
Heat capacity =m×s=8−J^∘C
(dthηdt)∈creases=2∘Cs
(dthηdt)decreases=0.2∘Cs
(a) Powerofheater=mS(dthηdt)∈creases
=80×2=160W
(b) Power of radiated
=mS(dthηdt)+(decreases)
=80×0.2=16W.
(c) Now, m(dthη(dt)decreases=K(T−T0
⇒16=K(30−20)
⇒K+1610=1.6
Now (dthηdt)=K(T−T0)=1.6×(30−25)
=1.6×5=8W.
Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - OBJECTIVE II
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer
4 Videos
Similar Questions
In Newton's law of cooling dθdt=−k(θ−θ0) the constant k is proportional to .
View SolutionA hot body placed in air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being k times the temperature difference from the surrounding. Starting from t=0 , find the time in which the body will lose half the maximum heat it can lose.
View SolutionA hot body placed in air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being k times the temperature difference from the surrounding. Starting from t=0 , find the time in which the body will loss half the maximum heat it can lose.
View SolutionA body cools in a surrounding which is at constant temperature of θ0. Assume that it obeys Newton's law of colling. Its temperature θ is plotted against time t. Tangents are drawn to the curve at the points P(θ=θt) and Q(θ=θ2). These tangents meet the time axis at angles of ϕ2 and ϕ1, as shown
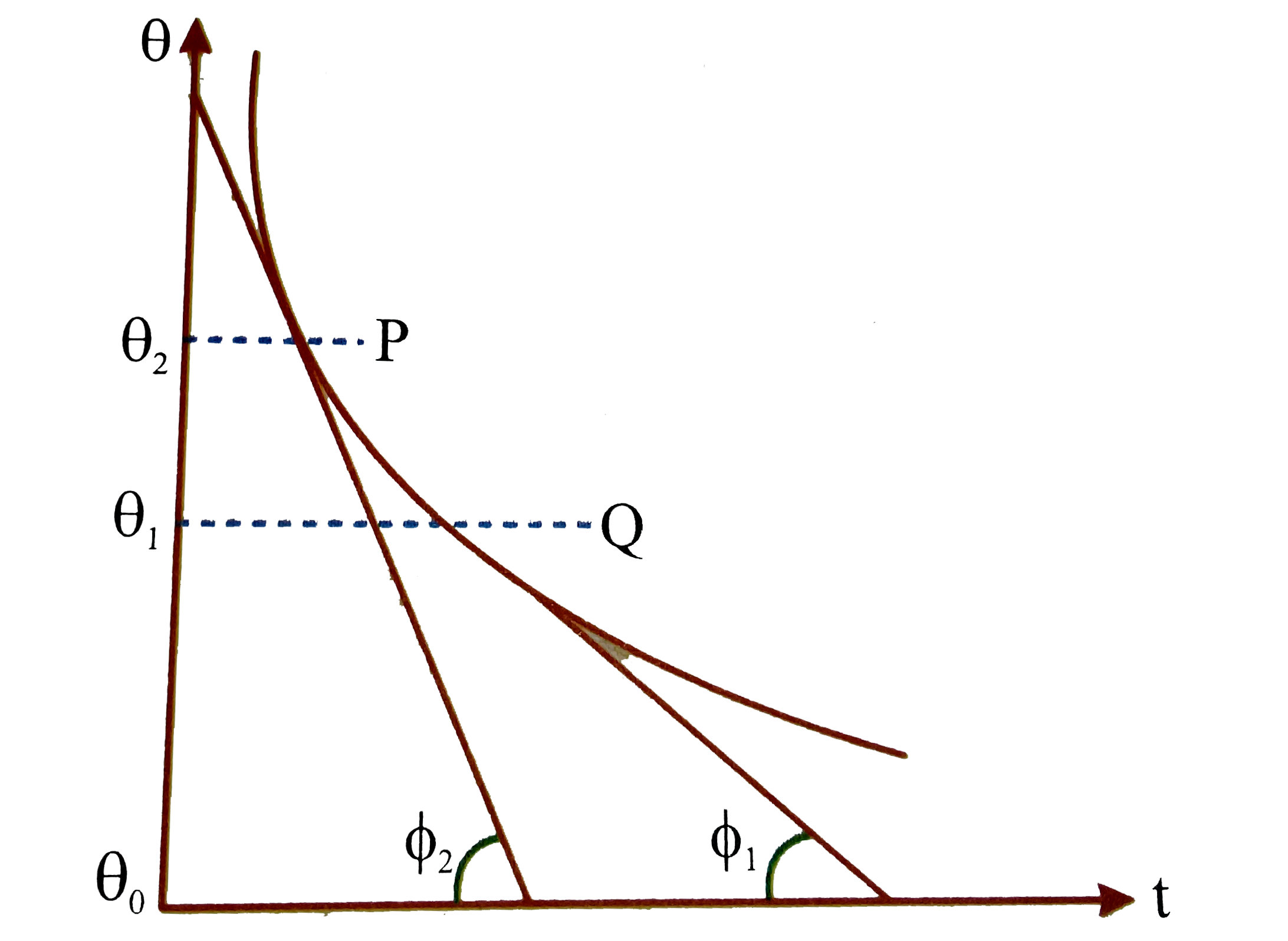
View SolutionDerive Newton's law of cooling to show that the rate of loss of heat from the body is proportional to the temperature difference between the body and its surroundings.
View SolutionA substance is in the solid from at 0∘C. The amount of heat added to this substance and its temperature is plotted in the graph . The specific heat capacity of the solid substance is 0.5cal//g∘C.
_E01_233_Q01.png)
The mass of the substance is -
View SolutionThemperature of a body θ is slightly more than the temperature of the surrounding θ0 its rate of cooling (R) versus temperature of body (θ) is plotted its shape would be .
View SolutionIf a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to
View Solution
A substance is in the solid form at 0∘C. The amount of heat added to this substance and its temperature are plotted in the following graph. If the relative specific heat capacity of the solid substance is 0.5, find from the graph (i) the mass of the substance, (ii) the specific latent heat of the melting process and (ii) the specific heat of the substance in the liquid state.
Specific heat capacity of water =1000cal/kg/K
View SolutionA body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ<θ1) Assume that Newton's law of cooling is obeyed Let k= constant The temperature of the body after time t is best experssed by .
View Solution
