A student is studying a book placed near the edge of a circular table of radius R. A point source of light is suspended directly above the centre of the table. What should be the height of the source above the table so as to produce maximum illuminance at the position of the book ?
The correct Answer is:B
To solve the problem of finding the height h of the point source of light above the table that produces maximum illuminance at the position of the book, we can follow these steps:
Step 1: Understand the Geometry
We have a circular table with radius R and a point source of light suspended directly above the center of the table at height h. The book is placed at the edge of the table.
Step 2: Define the Illuminance Formula
The illuminance E at a point on the table is given by the formula:
E=I0cosθd2
where I0 is the intensity of the light source, θ is the angle between the light ray and the normal to the surface, and d is the distance from the light source to the point on the table.
Step 3: Relate cosθ to Height and Radius
From the geometry of the situation, we can relate cosθ to the height h and the radius R using:
cosθ=h√R2+h2
This represents the vertical component of the light intensity.
Step 4: Calculate the Distance d
The distance d from the light source to the edge of the table (where the book is) can be calculated using the Pythagorean theorem:
d=√R2+h2
Step 5: Substitute into the Illuminance Formula
Substituting cosθ and d into the illuminance formula gives:
E=I0⋅h√R2+h2R2+h2
This simplifies to:
E=I0h(R2+h2)3/2
Step 6: Maximize the Illuminance
To find the height h that maximizes E, we need to take the derivative of E with respect to h and set it to zero:
dEdh=0
Using the quotient rule for differentiation, we differentiate E.
Step 7: Solve the Derivative Equation
After differentiating and simplifying, we arrive at the equation:
R2−2h2=0
This implies:
R2=2h2
Solving for h gives:
h=R√2
Final Answer
Thus, the height h of the source above the table for maximum illuminance at the position of the book is:
h=R√2
---
We have a circular table with radius R and a point source of light suspended directly above the center of the table at height h. The book is placed at the edge of the table.
The illuminance E at a point on the table is given by the formula:
E=I0cosθd2
where I0 is the intensity of the light source, θ is the angle between the light ray and the normal to the surface, and d is the distance from the light source to the point on the table.
From the geometry of the situation, we can relate cosθ to the height h and the radius R using:
cosθ=h√R2+h2
This represents the vertical component of the light intensity.
The distance d from the light source to the edge of the table (where the book is) can be calculated using the Pythagorean theorem:
d=√R2+h2
Substituting cosθ and d into the illuminance formula gives:
E=I0⋅h√R2+h2R2+h2
This simplifies to:
E=I0h(R2+h2)3/2
To find the height h that maximizes E, we need to take the derivative of E with respect to h and set it to zero:
dEdh=0
Using the quotient rule for differentiation, we differentiate E.
After differentiating and simplifying, we arrive at the equation:
R2−2h2=0
This implies:
R2=2h2
Solving for h gives:
h=R√2
Thus, the height h of the source above the table for maximum illuminance at the position of the book is:
h=R√2
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - question for short answer
13 Videos
- SEMICONDUCTOR AND SEMICONDUCTOR DEVICESBOOK - HC VERMA ENGLISHCHAPTER - SEMICONDUCTOR AND SEMICONDUCTOR DEVICESEXERCISE - Question for short answer
11 Videos
Similar Questions
A student is studying a book placed near the edge of a circular table of radius R. A point source of light is suspended directly above the centre of the table. What should be the height of the source above the table so as to produce maximum illuminance at the position of the book ?
View SolutionA uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly above the centre of the face, at a height 3a4 above the base. What is the minimum value of F for which the cube begins to tip about an edge?
View SolutionA plane mirror of circular shape with radius r=20cm is fixed to the ceiling .A bulb is to be placed on the axis of the mirror.A circular area of radius R=1m on the floor is to be illuminated after reflection of light from the mirror. The height of the room is 3m What is maximum distance from the center of the mirror and the bulb so that the required area is illuminated?
View SolutionA: When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle.
R: Waves diffracted from the edge of the circular obstacle interfere constructively at the centre of the shadow producing a bright spot.
View SolutionA uniform cube of side 'a' and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly below the centre of the face, at a height a/4 above the base.
a. What is the minimum value of F for which the cube begins to tip about an edge?
b. What is the minimum value of its so that toppling occurs?
c. If μ=μmin find minimum force for topping.
d. Find minimum μs so that Fmin can cause toppling.
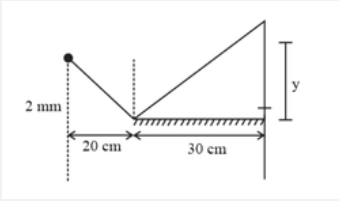
View SolutionA plane mirror of length 30 cm is placed horizontally along with a vertical screen. A monochromatic point source of light is placed 20 cm to the left off the left edge of the mirror, at a height of 2 mm above the plane of the mirror. If the wavelength of light used is 6400Å, then find the number of complete bright fringes formed.
View SolutionInside a solid glass sphere of radius R, a point source of light lies at a distance x(x<R) from centre of the sphere. The solid is surrounded by air of refractive index 1. The maximum angle of incidence for rays incident on the spherical glass air interface directly from the point soure is:
View SolutionAn air puck of mass m1 is tied to a string allowed to revolved in a circle of radius R on a frictionless horizontal table . The other end of the string passes through a small hole in the centre of the table , and a load of mass m2 is tied to the string? The suspended load remains in equilibrium while the pack on the tabletop revolves.

a. Find the tension in the string
b. Find the radial force acting on the puck
c. Find the speed of the puck
d. Qualitaively describe what will happen in the motion of the puck if the value of m2 is somewhat increased by placing an additional load on it.
e.Qualitaively describe what will happen in the motion of the puck if the value of m2 is instead decreased removing a part from the hanging load.
View SolutionA point source of light moves ijn a straight line paralel to a plane table. Consider a small portion of the table directly below the line of movement of the source. The illuminance at this portion varies with its distasnce r from the source as
View SolutionA glass sphere has radius of 5.0cm and a refractive index of 1.6. A paperweight is constructed by slicing through the sphere on a plate that is 2.0cm from the centre of the sphere and perpendicular to radius of the sphere that passes through the centre of the circle formed by the intersection of the plane and the sphere. The paperweight is placed on a table and viewed from directly above an observer who is 8.0cm from the table top, as shown in figure. When viewed through the paperweight, how far away does the table top appear to the observer?
View Solution
