A uniform cube of side 'a' and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly below the centre of the face, at a height a/4 above the base.
a. What is the minimum value of F for which the cube begins to tip about an edge?
b. What is the minimum value of its so that toppling occurs?
c. If μ=μmin find minimum force for topping.
d. Find minimum μs so that Fmin can cause toppling.
The correct Answer is:2
a. In the limiting case normal reaction will pass through O. The cube will tip about O if torque of F about O exceeds the torque of mg
Hence F(a4)>mg(a2)
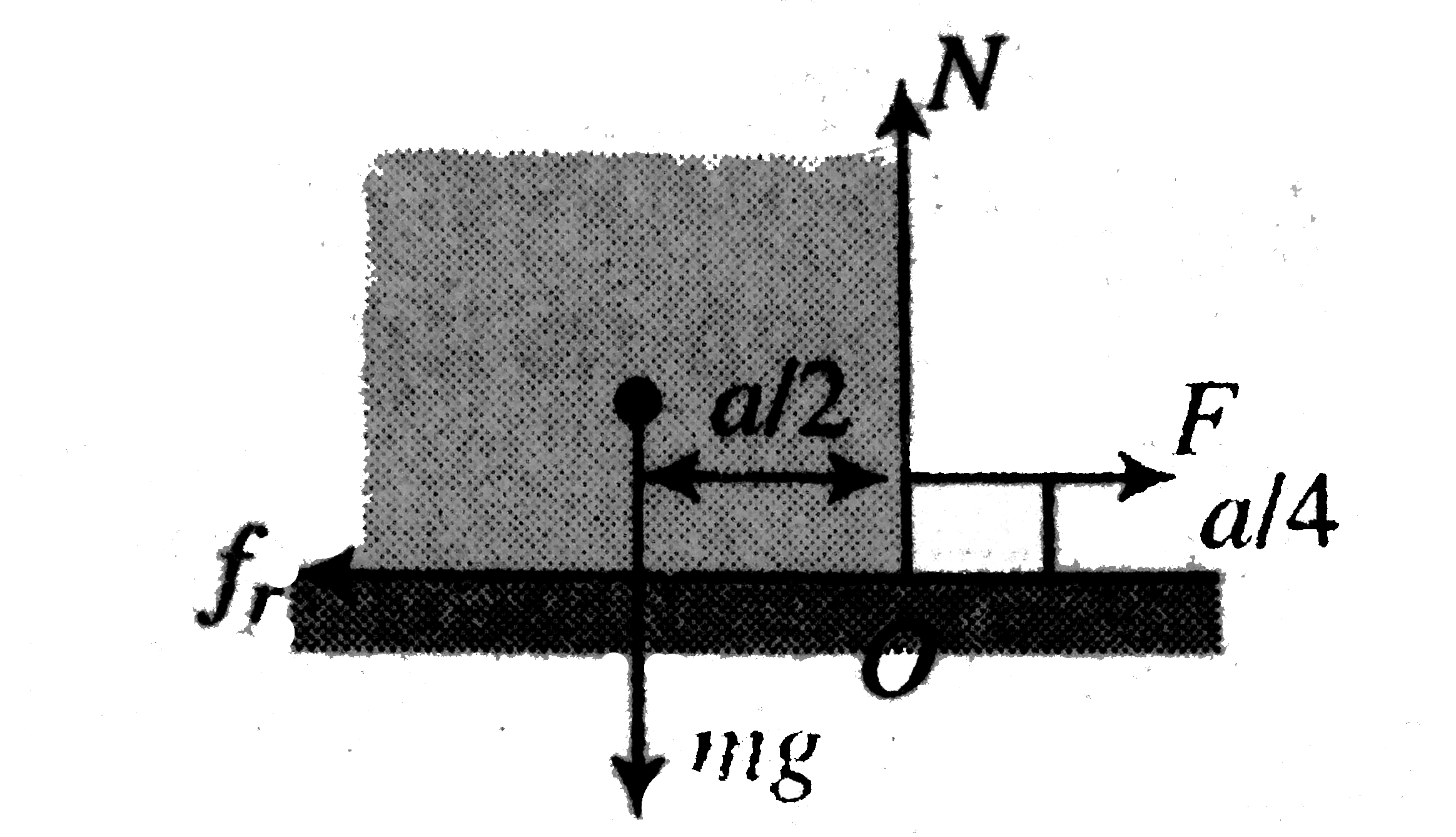
or F>mg
Therefore minimum value of F is 2mg
b. In this case since it is not acting at COM,
toppling can occur even after body started sliding because increasing the torque of F about COM. Hence μmin=0,
c. Now body is sliding before toplling O is not IAR, torque equation can not be applied across it. It can now be applied about COM.
F×a4=N×a2 ......i
N=mg ...........ii
From i and ii
F=2mg
d. F>2mg ............iii
from sol a
N=mg
FμsN=μsmg.........iv
from i and ii μs=2.......v
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct97videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.411videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly above the centre of the face, at a height 3a4 above the base. What is the minimum value of F for which the cube begins to tip about an edge?
View SolutionA uniform cube of side and mass m rests on a rough horizontal surface. A horizontal force F is applied normal to one face at point that is directly above the centre of the face at a height a4 above the centre. The minimum value of F for which the cube begins to topple above an edge without sliding is
View SolutionIf the friction is sufficient to prevent the block from sliding, then the minimum value of F for which the cube begins to topple about an edge is
 View Solution
View SolutionA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force F is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is
 View Solution
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isView Solution
A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,View SolutionA uniform sphere is place on a smooth horizontal surface and as horizontal force F is appied on it at a distance h above the surface. The acceleratioin of the centre
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View SolutionA unifrom cube of mass m and side a is placed on a frictionless horizontal surface .A vertical force F is applied to the edge as shown in figure ,match the following (most appropriate choice )
 View Solution
View SolutionThree identical cubes each of mass m are place on a smooth horizontal surface.A constant force F is applied on A as shown in the figure.The force on B applied by C is
View Solution
