The displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given by f(t)=Asin(tT). The wave speed is v. Write the wave equation.
The correct Answer is:A
To derive the wave equation from the given displacement function, we can follow these steps:
Step 1: Understand the given displacement function
The displacement of the particle at x=0 is given by:
f(t)=Asin(tT)
where A is the amplitude, t is the time, and T is the time period.
Step 2: Identify the wave speed and its relationship with wavelength and frequency
The wave speed v is related to the wavelength λ and frequency ν by the equation:
v=λν
Frequency ν can also be expressed as:
ν=1T
Thus, we can rewrite the wave speed equation as:
v=λ⋅1T
Rearranging this gives:
λ=vT
Step 3: Write the general form of the wave equation
The general form of a wave traveling in the positive x-direction can be expressed as:
y(x,t)=Asin(2πλx−ωt)
where ω is the angular frequency given by:
ω=2πT
Step 4: Substitute the values into the wave equation
From the previous steps, we have:
- λ=vT
- ω=2πT
Substituting these into the wave equation gives:
y(x,t)=Asin(2πvTx−2πTt)
Step 5: Simplify the wave equation
Since 2πT can be factored out, we rewrite the wave equation as:
y(x,t)=Asin(2πvTx−2πTt)
This can be expressed in terms of the wave speed v:
y(x,t)=Asin(2πλx−2πTt)
where λ=vT.
Final Wave Equation
Thus, the wave equation is:
y(x,t)=Asin(2πvTx−2πTt)
The displacement of the particle at x=0 is given by:
f(t)=Asin(tT)
where A is the amplitude, t is the time, and T is the time period.
The wave speed v is related to the wavelength λ and frequency ν by the equation:
v=λν
Frequency ν can also be expressed as:
ν=1T
Thus, we can rewrite the wave speed equation as:
v=λ⋅1T
Rearranging this gives:
λ=vT
The general form of a wave traveling in the positive x-direction can be expressed as:
y(x,t)=Asin(2πλx−ωt)
where ω is the angular frequency given by:
ω=2πT
From the previous steps, we have:
- λ=vT
- ω=2πT
y(x,t)=Asin(2πvTx−2πTt)
Since 2πT can be factored out, we rewrite the wave equation as:
y(x,t)=Asin(2πvTx−2πTt)
This can be expressed in terms of the wave speed v:
y(x,t)=Asin(2πλx−2πTt)
where λ=vT.
Thus, the wave equation is:
y(x,t)=Asin(2πvTx−2πTt)
Topper's Solved these Questions
- WAVE MOTION AND WAVES ON A STRINGBook:HC VERMA ENGLISHChapter:WAVE MOTION AND WAVES ON A STRINGExercise:Question for short Answer
Explore 7 Videos
- WAVE MOTION AND WAVES ON A STRINGBook:HC VERMA ENGLISHChapter:WAVE MOTION AND WAVES ON A STRINGExercise:Objective -2
Explore 9 Videos
- THE FORCESBook:HC VERMA ENGLISHChapter:THE FORCESExercise:Questions for short Answer
Explore 9 Videos
- WORK AND ENERGYBook:HC VERMA ENGLISHChapter:WORK AND ENERGYExercise:Question for Short Answer
Explore 16 Videos
Similar Questions
The displacement of A particle at x = 0 of a stretched string carrying a wave in the positive X-direction is given by f(t)=Ae−t2. The wave speed is V. Write equation of the wave.
View SolutionFigure shows a plot of the transverse displacement of the particle of a string at t=0 through which a travelling wave is passing in the positive in the positive x-direction. The wave speed is 20cm/s. Find (a) the amplitude (b) the wavelength (c) the wave number and (d) the frequency of the wave.

View Solution
Knowledge Check
The speed of transverse wave on a stretched string is
Adirectly proportional to the tension in the stringBdirectly proportional to the square root of the tensionCinversely proportional to liveDinversely proportional to sqyare of tension
Figure shows a plot of the transverse displacements of the particles of a string at t = 0 through which a travelling wave is passing in the positive x-direction. The wave speed is 20cms−1. Find (a) the amplitude, (b) the wavelength, (c) the wave number and (d) the frequency of the wave.
 .
.
View SolutionThe displacement of a particle of a string carrying a travelling wave is given by y=(3.0cm)sin6.28(0.50x−50t), where x is in centimetre and t in second Find (a) the amplitude, (b) the wavelength, (c ) the frequency and (d) the speed of the wave.
View SolutionA travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidal. The amplitude of vibration is 1.0cm and the displacement becomes zero 200 times per second. The linear mass density of the string is 0.10kgm−1 and it is kept under a tension of 90 N. (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive x-direction and at t = 0 the end x= 0 is at its positive extreme position. Write the wave equation. (c ) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10ms.
View Solutionthe equation of a wave travelling along the positive x - axis ,as shown in figure at t = 0 is given by

View SolutionThe equation of a wave travelling along the positive x-axis, as shown in figure at t = 0 is given by
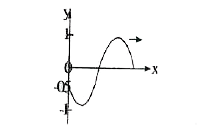
View SolutionThe displacement of a wave disturbance propagating in the positive x-direction is given by
y=11+x2at t=0 and y=11+(x−1)2 at t=2s
where, x and y are in meter. The shape of the wave disturbance does not change during the propagation. what is the velocity of the wave?
View SolutionA wave is propagating on a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)2
where y0=4mm,T=1.0sandλ=4cm.(a) find the velocity of wave. (b) find the function f(t) giving the displacement of particle at x=0. (c) find the function g(x) giving the shape of the string at t=0.(d) plot the shape g(x) of the string at t=0 (e) Plot of the shape of the string at t=5s.
View Solution

