If the road of the previous problem is horizontal (no banking), what should be the minimum friction coefficeint so that a scooter going at 18 km/hr does not skid?
The correct Answer is:B
To find the minimum coefficient of friction required for a scooter to navigate a turn without skidding, we can follow these steps:
Step 1: Identify the Forces Acting on the Scooter
When the scooter is taking a turn, the following forces are acting on it:
- The weight of the scooter and rider, mg, acting downwards.
- The normal force, N, acting upwards.
- The centrifugal force, which is the inertial force acting outward, given by mv2R, where m is the mass of the scooter and rider, v is the velocity, and R is the radius of the turn.
- The frictional force, which acts inward and is given by μN, where μ is the coefficient of friction.
Step 2: Set Up the Equations
From the forces acting on the scooter, we can establish the following equations:
1. The normal force N balances the weight:
N=mg
2. The frictional force must provide the necessary centripetal force to keep the scooter moving in a circle:
μN=mv2R
Step 3: Substitute the Normal Force
Substituting the expression for N from the first equation into the second equation gives:
μmg=mv2R
Here, we can cancel m from both sides (assuming m≠0):
μg=v2R
Step 4: Solve for the Coefficient of Friction
Rearranging the equation to solve for μ:
μ=v2gR
Step 5: Convert the Speed to Meters per Second
The speed given is 18 km/hr. We need to convert this to meters per second:
v=18 km/hr×1000 m1 km×1 hr3600 s=5 m/s
Step 6: Plug in the Values
Now we can substitute v=5 m/s, g=10 m/s2 (approximating the acceleration due to gravity), and R=30 m into the equation for μ:
μ=(5)210×30
Calculating this gives:
μ=25300=112≈0.0833
Final Answer
Thus, the minimum coefficient of friction required is approximately:
μ≈0.084
When the scooter is taking a turn, the following forces are acting on it:
- The weight of the scooter and rider, mg, acting downwards.
- The normal force, N, acting upwards.
- The centrifugal force, which is the inertial force acting outward, given by mv2R, where m is the mass of the scooter and rider, v is the velocity, and R is the radius of the turn.
- The frictional force, which acts inward and is given by μN, where μ is the coefficient of friction.
From the forces acting on the scooter, we can establish the following equations:
1. The normal force N balances the weight:
N=mg
2. The frictional force must provide the necessary centripetal force to keep the scooter moving in a circle:
μN=mv2R
Substituting the expression for N from the first equation into the second equation gives:
μmg=mv2R
Here, we can cancel m from both sides (assuming m≠0):
μg=v2R
Rearranging the equation to solve for μ:
μ=v2gR
The speed given is 18 km/hr. We need to convert this to meters per second:
v=18 km/hr×1000 m1 km×1 hr3600 s=5 m/s
Now we can substitute v=5 m/s, g=10 m/s2 (approximating the acceleration due to gravity), and R=30 m into the equation for μ:
μ=(5)210×30
Calculating this gives:
μ=25300=112≈0.0833
Thus, the minimum coefficient of friction required is approximately:
μ≈0.084
Topper's Solved these Questions
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Question for short Answer
Explore 10 Videos
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Objective -2
Explore 6 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBook:HC VERMA ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONExercise:Objective -2
Explore 11 Videos
- FLUID MECHANICSBook:HC VERMA ENGLISHChapter:FLUID MECHANICSExercise:All Questions
Explore 90 Videos
Similar Questions
If the road of the previous problem is horizontal (no banking), what should be the minimum friction coefficient so that a scooter going at 18km/h does not skid?
View SolutionIf the road is horizontal (no banking), what should be the minimum friction coefficeint so that a scooter going at 18 km/hr does not skid for r=10m ?
View SolutionA track consists of two circular pars ABC and CDE of equal radius 100 m and joined smoothly as shown in figure.Each part subtends a right angle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Find the normal contact force by the road on the cycle when it is at B and at D. b.Find the force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between the road and the cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g=10ms2

View SolutionA track consists of two circular pars ABC andCDE of equal rdius 100 m and joined smoothly as shown in figure.Each part sutends a right ngle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Findteh nromal contct force by tehroad on the cycle whenit is at B and at D. b.Findteh force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between teh road and teh cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that teh cyclist can move with constant speed? Take g=10ms2

View SolutionA car goes on a circular horizontal road of radius 100 m. What should be the minimum coefficient of friction between the tyres and the road so that it completes the circle with velocity 10 m/s without slipping ? (Take g=10m/s2)
View SolutionA sphere of mass M rolls without slipping on the inclined plane of inclination θ. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping ?
View SolutionThe length of a uniform ladder of mass m is 1. It leans against a smooth wall making an angle θ with the horizontal. What should be the force of friction between the floor and ladder so that the ladder does not slip ?
View SolutionA bucket tied at the end of a 1.6m long string is whirled in a verticle circle with constant speed. What should be the minimum speed so that the water from the bucket does not spill, when the bucket is at the highest position (Takeg=10m/s2)
View SolutionA block of mass M=4kg of height and breath b is placed on a rough plank of same mass M. A light inextensible string is connected to the upper end of the block and passed through a light smooth pulley as shown in figure. A mass m=1kg is hung to the other end of the string.
a. What should be the minimum value of coefficient of friction between the block and the plank so that, there is no slipping between the block and the wedge?
b. Find the minimum value of b/h so that the block does not topple over the plank, friction is absent between the plank and the ground.

View SolutionAt the bottom edge of a smooth wall, an inclined plane is kept at an angle of 45∘. A uniform ladder of length l and mass M rests on the inclined plane against the wall such that it is perpendicular to the incline.
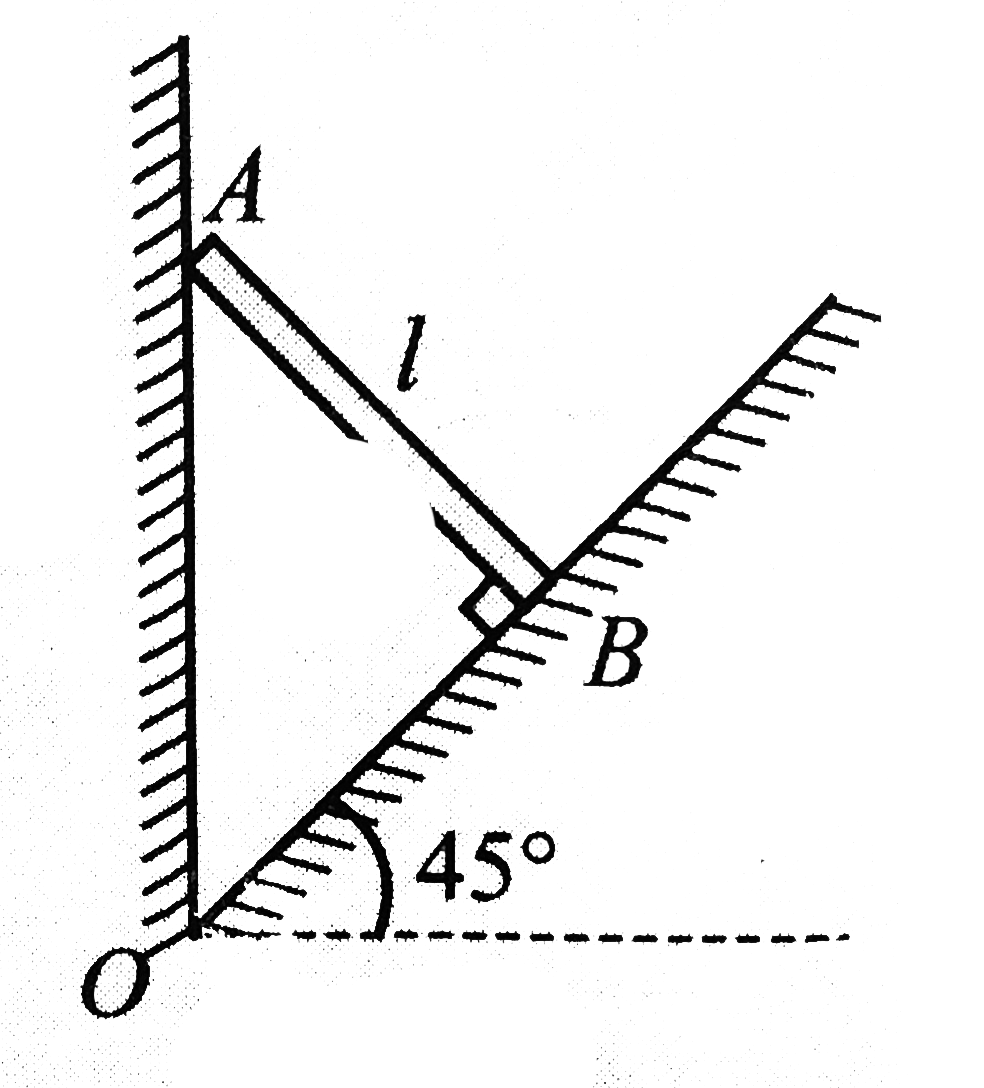
a. If the plane is also smooth, which way will the ladder slide?
b. What is the minimum coefficient of friction necessary so that the ladder does not slip on the incline.
View Solution