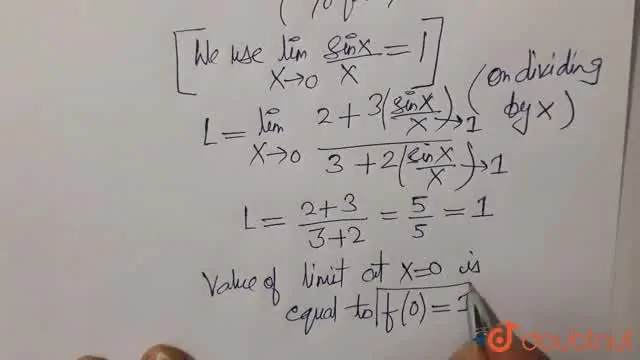If f(x)=2x+3sinx3x+2sinx , x≠0 is continuous at x=0 , then find f(0)
Step by step video & image solution for If f(x)=(2x+3sinx)/(3x+2sinx) , x!=0 is continuous at x=0 , then find f(0) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
If f(x)=4+sin2x+asinx+Bcosxx2 for x≠0 is continuous at x=0, then A+B+f(0) is
View SolutionIf f(x)=sin3x+Asin2x+Bsinxx5 forx≠0 is continuous at x=0, then A+B+f(0) is
View SolutionIf the function f(x)=tan(tanx)−sin(sinx)tanx−sinx(x≠0): is continuous at x=0,then find the value of f(0)
View SolutionIf the function f(x)=x(esinx−1)1−cosx is continuous at x =0 then f(0)=
View SolutionThe function f(x)={sinxx+cosx,x≠0 and f(x) =k at x=0 is continuous at x=0 then find the value of k
View SolutionIf f(x)=(1−tanx1+sinx)cosecx is to be made continuous at x=0, then f(0) must be equal to
View SolutionThe function f(x)=(3x−1)2sinx⋅ln(1+x),x≠0, is continuous at x=0, Then the value of f(0) is
View SolutionIf f(x)=[aesinx+be−sinx−cx2x≠02x=0 is continous at x=0, then:
View SolutionProve that f(x)={sinxx;x≠0and1;x=0. is continuous at x=0.
View SolutionIf f(x)=f(x)={sin(a+1)x+sinxx,,x<0,c atx=0,√x+bx2−√xbx√x,x≥0,f(x) is continuous at x=0,then (a).a=−32,b=0,c=12 (b) a=−32,b=1,c=−12 (c)a=−32,b∈R−[0],c=12 (d) none of these
View Solution