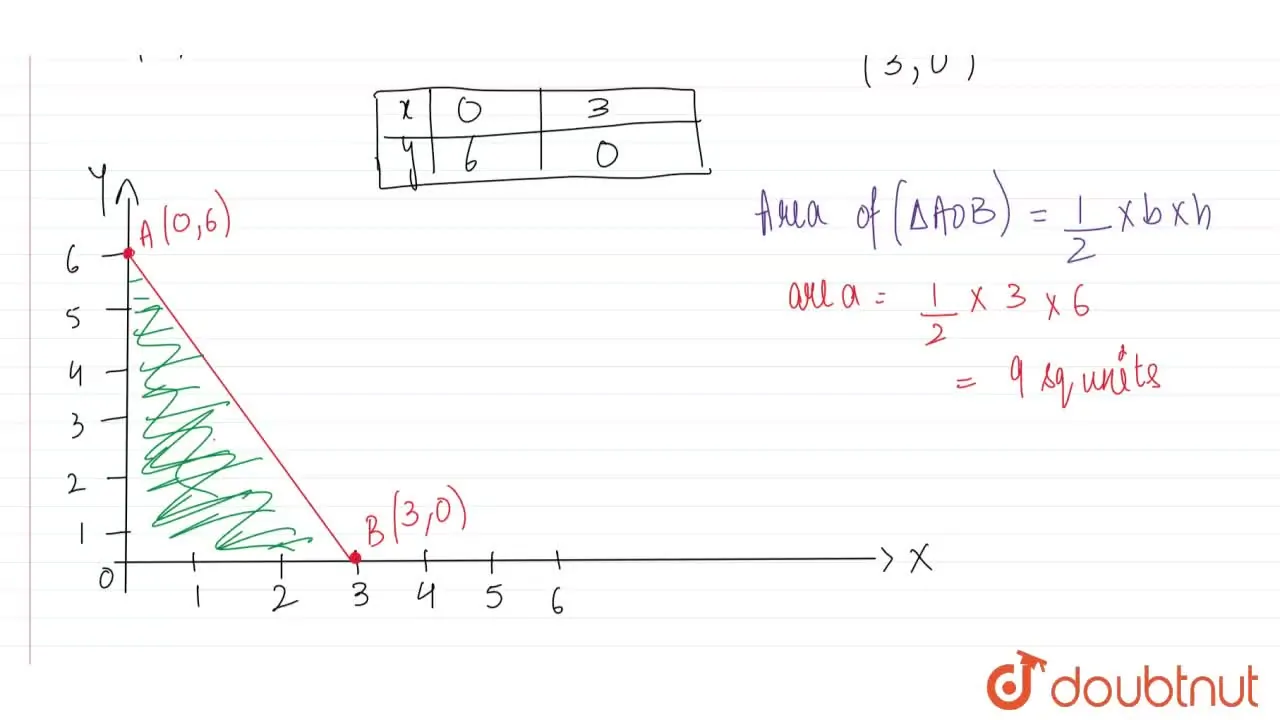
Draw the graph of the equation 2x+y=6 . Shade the region bounded by the graph and the coordinate axes. Also, find the area of the shaded region.
Step by step video & image solution for Draw the graph of the equation 2x+y=6 . Shade the region bounded by the graph and the coordinate axes. Also, find the area of the shaded region. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
Similar Questions
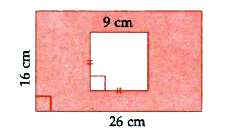
Find the area of the shaded region in figure.
 View Solution
View SolutionFind the area of the shaded region in Figure.
View SolutionIn the joining figure , find the area of the shaded region.
 View Solution
View SolutionDraw the graphs of 2x+y=6andx−y+2=0. Shade the region boun-ded by these lines and x=axis. Find the area of the shaded region.
View SolutionDraw the graphs of 2x+y=6 and 2x−y+2=0 . Shade the region bounded by these lines and x-axis. Find the area of the shaded region.
View SolutionDraw the graphs of the equations x−y=1 and 2x+y=8 . Shade the area bounded by these two lines and y-axis. Also, determine this area.
View SolutionDraw the graph of the equation x3+y4=1. Also, find the area of the triangle formed by the line and the coordinates axes.
View SolutionFind the area of the shaded region given in figure.
 View Solution
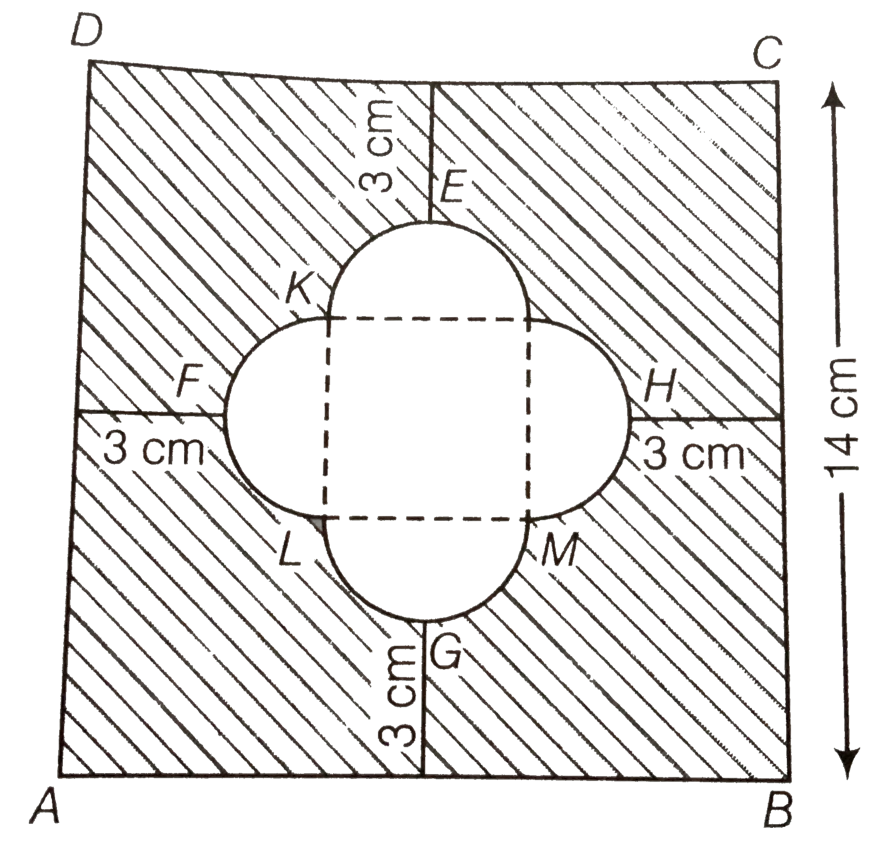
View SolutionIn the given figure, find the area of the shaded region [Useπ=3.14]
View SolutionIn figure, find the area of the shaded region [Useπ=3.14]
View Solution