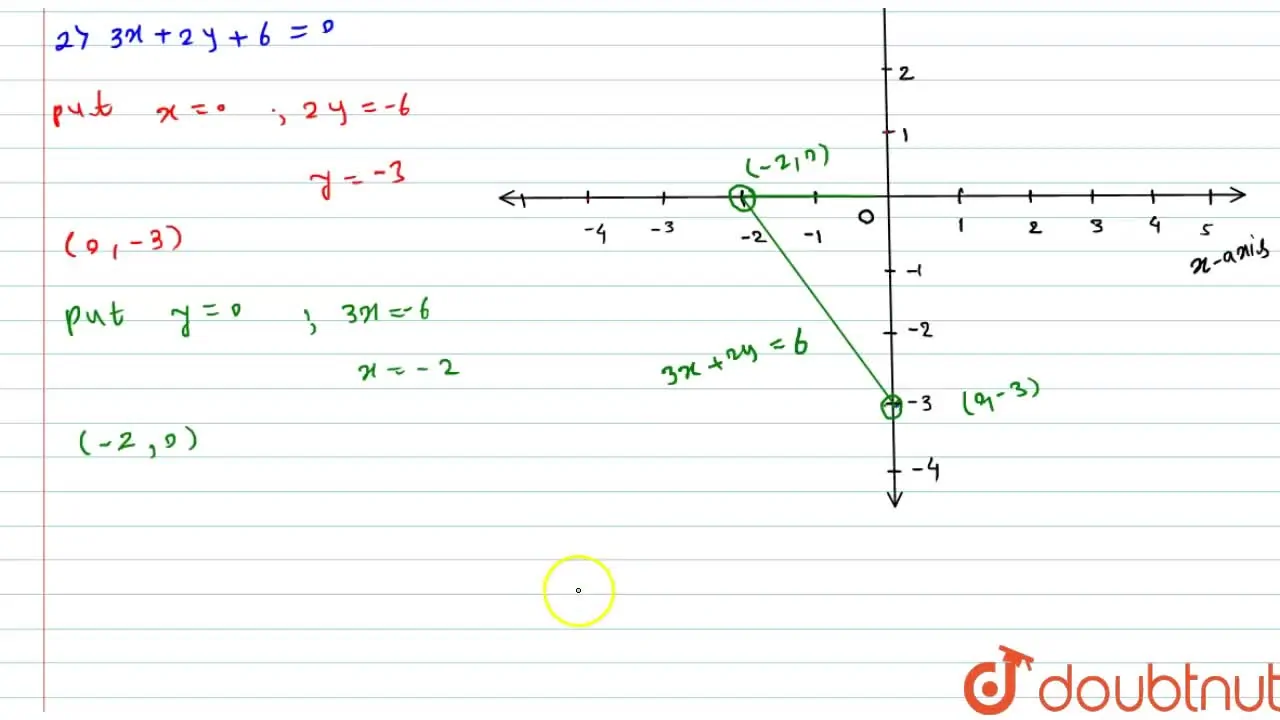
Draw the graph of each of the equations given below. Also, find the coordinates of the points where the graph cuts the coordinate axes: 2x+y=6 (ii) 3x+2y+6=0
Step by step video & image solution for Draw the graph of each of the equations given below. Also, find the coordinates of the points where the graph cuts the coordinate axes: 2x+y=6 (ii) 3x+2y+6=0 by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
Similar Questions
Draw the graph of each of the equations given below. Also, find the coordinates of the points where the graph cuts the coordinate axes: 6x−3y=12 (ii) −x+4y=8
View SolutionDraw the graph for each equation given below, hence find the co-ordinate of the points when the graph drawn meets the co-ordinate axes:
13x+15y=1View SolutionDraw the graph for each linear equation given below:
y=xView SolutionDraw the graph for each linear equation given below:
y=0View SolutionDraw the graph for each linear equation given below:
y=3xView SolutionDraw the graph for each equation given below, hence find the co-ordinate of the points when the graph drawn meets the co-ordinate axes:
2x+153=y−1View SolutionDraw the graph for each linear equation given below:
y=−xView SolutionDraw the graph for each linear equation given below:
y+6=0View SolutionDraw the graph for each linear equation given below:
x=−2yView SolutionDraw the graph for each linear equation given below:
y=−2xView Solution