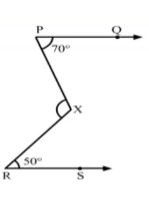
If Figure, if QT⊥PR,∠TQR=400 AND ∠SPR=300, find x and y. Figure
To solve the problem, we will follow these steps:
Step 1: Analyze Triangle TQR
We know that QT is perpendicular to PR, which means that ∠QTR=90∘. We are also given that ∠TQR=40∘. We need to find ∠TRQ (denoted as x).
Step 2: Apply the Angle Sum Property
According to the angle sum property of triangles, the sum of all angles in a triangle is 180∘. Therefore, we can write the equation for triangle TQR:
∠TQR+∠QTR+∠TRQ=180∘
Substituting the known values:
40∘+90∘+x=180∘
Step 3: Solve for x
Now, we simplify the equation:
130∘+x=180∘
Subtract 130∘ from both sides:
x=180∘−130∘=50∘
Step 4: Analyze Triangle PSR
Next, we will find y (denoted as ∠PSQ). In triangle PSR, we can use the exterior angle property. Here, ∠PSQ (denoted as y) is the exterior angle for triangle PSR.
Step 5: Apply the Exterior Angle Property
The exterior angle property states that the exterior angle is equal to the sum of the two opposite interior angles. Thus, we can write:
y=∠SPR+∠PRS
We know that ∠SPR=30∘ and we just found that ∠PRS=x=50∘. Therefore:
y=30∘+50∘
Step 6: Solve for y
Now, we can calculate y:
y=80∘
Final Results
Thus, we have found:
- x=50∘
- y=80∘
We know that QT is perpendicular to PR, which means that ∠QTR=90∘. We are also given that ∠TQR=40∘. We need to find ∠TRQ (denoted as x).
According to the angle sum property of triangles, the sum of all angles in a triangle is 180∘. Therefore, we can write the equation for triangle TQR:
Now, we simplify the equation:
Next, we will find y (denoted as ∠PSQ). In triangle PSR, we can use the exterior angle property. Here, ∠PSQ (denoted as y) is the exterior angle for triangle PSR.
The exterior angle property states that the exterior angle is equal to the sum of the two opposite interior angles. Thus, we can write:
Now, we can calculate y:
Thus, we have found:
- y=80∘
Topper's Solved these Questions
Similar Questions
In Fig. 6.37, if QT⊥PR,∠TQR=40∘and∠SPR=30∘, find x and y.
View SolutionIn Figure, if QT⊥PR, ∠TQR=40∘ and ∠SPR=30∘, find x and y.
View SolutionIn figure, if PQ⊥PS,PQ∣∣SR,∠SQR=280 and ∠QRT=650, then find the values of x and y. Figure
View SolutionIn Figure, if PQ⊥PS, PQSR, ∠SQR=280and ∠QRT=650, then find the values of x and y
View SolutionIn Figure, if PQ∣∣RS, ∠MXQ=135∘and ∠MYR=40∘,find ∠XMY
View SolutionIn Fig. if ST∣∣QR . Find PS
View SolutionIn Figure , find out ∠PXR, if PQ ∣∣ RS.
View SolutionIn Figure, OP∣∣RS. Determine ∠PQR
View SolutionIn Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.

View SolutionIn figure, if lines PQ and RS intersect at a point T such that PRT=400,∠RPT=950 and ∠TSQ=750, find ∠SQT. Figure
View Solution
