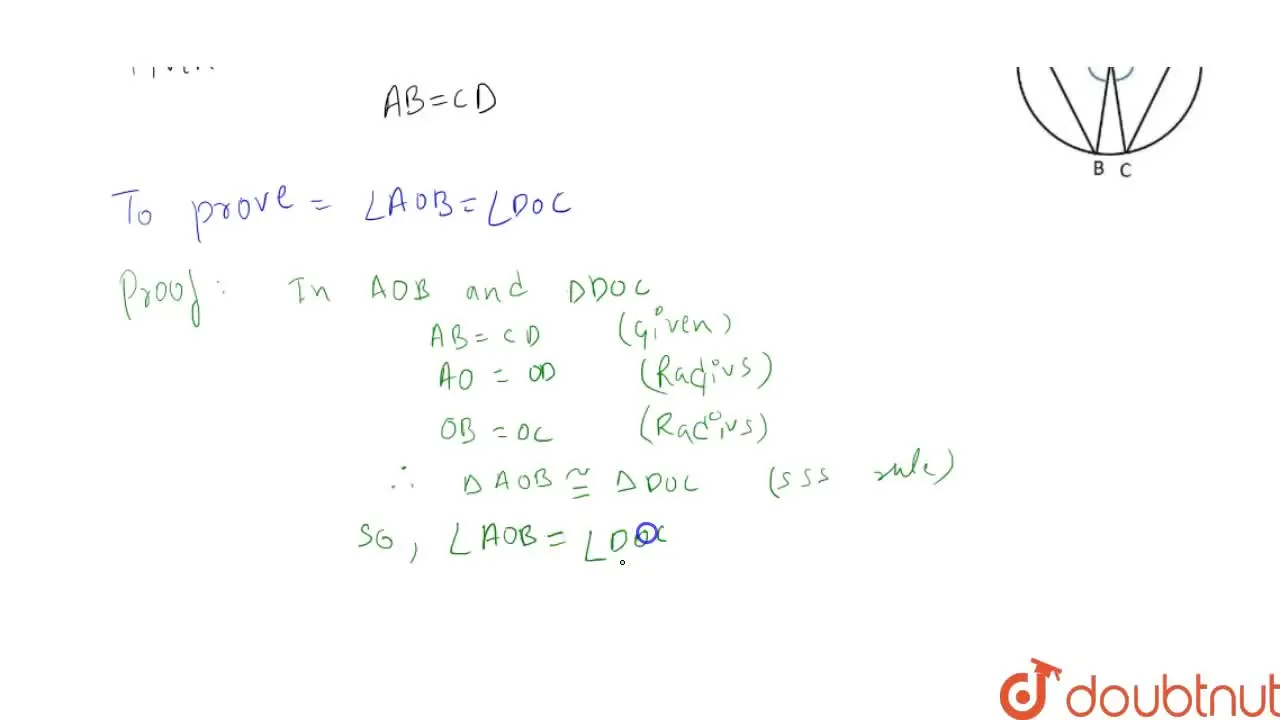Prove Equal chords of a circle subtend equal angles at the centre.
Step by step video & image solution for Prove Equal chords of a circle subtend equal angles at the centre. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
Similar Questions
Prove Equal chords of congruent circles subtend equal angles at the centre.
View Solutionprove that the line joining the mid-point of two equal chords of a circle subtends equal angles with the chord.
View SolutionProve that equal chords of congruent circles subtend equal angles at their centre.
View SolutionProve that equal chords of congruent circles subtend equal angles at their centre.
View SolutionProve that if chords of congruent circles subtend equal angles at their centres, thenthe chords are equal.
View Solutionr : Two chords of a circle subtend equal angles at centre if and only if they are equal.
Statement r can be interpreted asView SolutionEqual chords of a circle are equidistant from the centre.
View SolutionProve that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
View SolutionLet α chord of a circle be that chord of the circle which subtends an angle α at the center.
If x+y=1 is a chord of x2+y2=1, then α is equal toView SolutionProve that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the centre.
View Solution