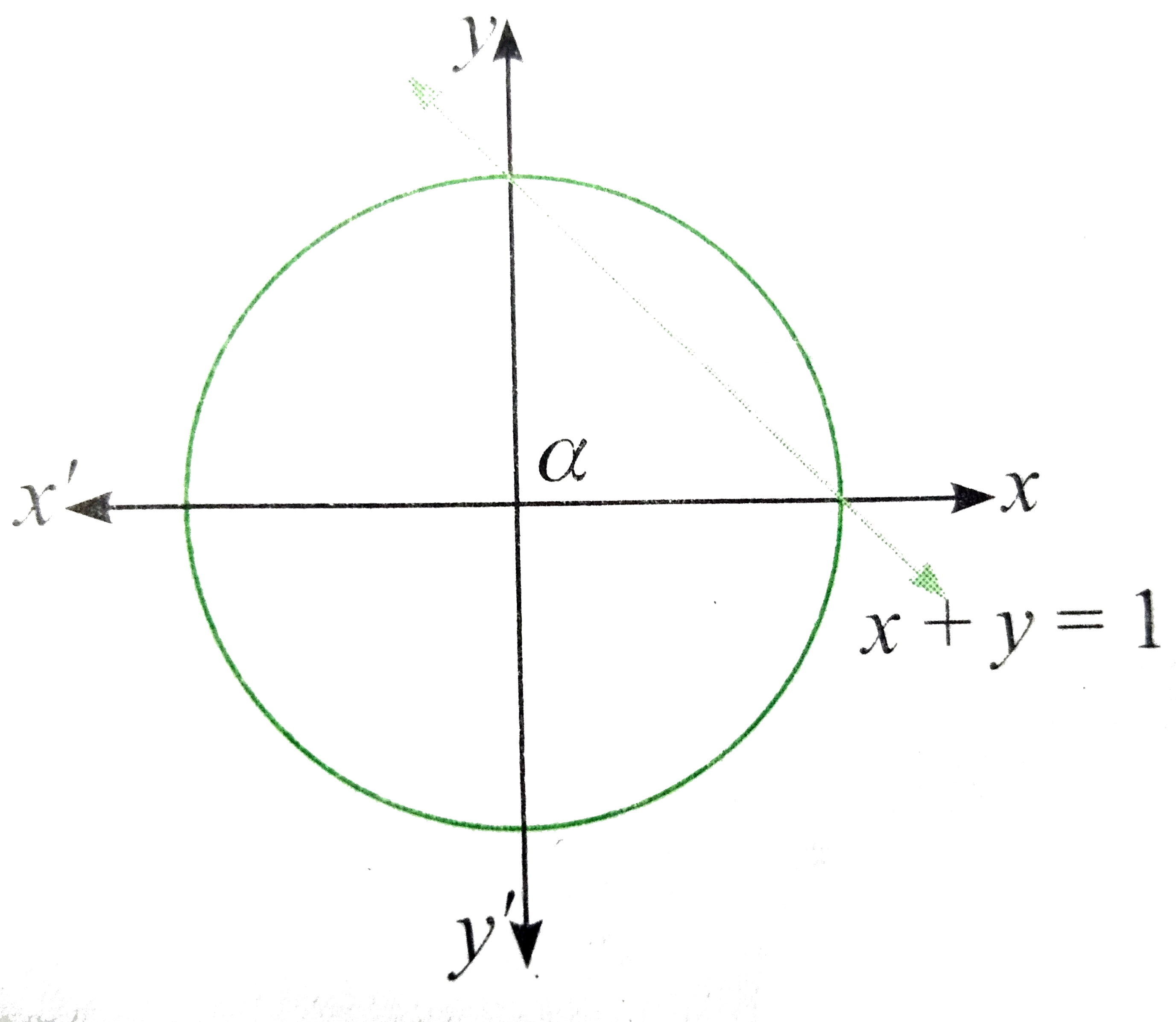
Let chord of a circle be that chord of the circle which subtends an angle at the center.
If is a chord of , then is equal to
is not a chord
The correct Answer is:2
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - NUMERICAL VALUE TYPE
21 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - ARCHIVES (JEE MAIN)
1 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Let α chord of a circle be that chord of the circle which subtends an angle α at the center.
If the slope of a π/3 chord of x2+y2=4 is 1, then its equation is
View SolutionLet α chord of a circle be that chord of the circle which subtends an angle α at the center.
The distance of 2π/3 chord of x2+y2+2x+4y+1=0 from the center is
View SolutionProve Equal chords of a circle subtend equal angles at the centre.
View SolutionProve Equal chords of congruent circles subtend equal angles at the centre.
View SolutionProve that equal chords of congruent circles subtend equal angles at their centre.
View SolutionProve that equal chords of congruent circles subtend equal angles at their centre.
View SolutionThe chord of a circle is equal to its radius, find the angle subtended by this chord at the centre.
View SolutionThe locus of the mid-points of the chords of the circle x2+y2−2x−4y−11=0 which subtends an angle of 60∘ at center is
View SolutionProve that if chords of congruent circles subtend equal angles at their centres, thenthe chords are equal.
View SolutionFind the locus of the midpoint of the chord of the circle x2+y2−2x−2y=0 , which makes an angle of 1200 at the center.
View Solution