The lower corner of a leaf in a book is folded over so as to reach the inner edge of the page. Show that the fraction of the width folded over when the area of the folded part is minimum is:
Let the corner A of the leaf ABCD be folded over to A Which is one the inner edge BC of the page.
Let AP=x and AB=a. Therefore,BP=a-x

If∠APB==θthen∠EA'F=θ.EF is parallel to AB, then EF=a.
In △A'BP,cosθ=BPPA'=a−xx
In △A'FE,A'E=EFcosecθ=a/√1−cos2θ
=a/
⎷1−{a−x}{x}2
=(ax)√x2−(a−x)2=ax√2ax−a2=aE
Triangle APe is folded to triangle A'PE .Therefore,
Area of folded part=Area of △PAE=12AP.AE
=12xax√2ax−a2=A (say)
or A2=a2x44(2ax−a2)=a2/42a/x3−a2/x4=a2/4y
where y=(2a/x3)−a2/x4,0<x<a
ObviouslyA2 (i.e,A) is minimum when y is maximum .Now,
y=2a/x3−a2/x4
or dydx=−6ax4+4a2x5andd2ydx2andd2ydx2=24ax5−20a2x6
For maximum or mnimum of y,
ddx=−6ax4+4a2x5=0orx=2a/3
When x=2a/3,−6ax45+4a2x5=0orx=2a/3
when x=2a/3,d2ydx2=4ax5(6−5ax)
=4a3(2a)56−5a32a=−4a3(2a)532<0
Thus y is maximum i.e A is minimum when x=2a/3 which is the only criticla point (least).Hence the folded area is minimum when 2/3 of the width of the page is folded over.
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.1
10 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.2
10 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Matrix Match Type
14 Videos
- METHODS OF DIFFERENTIATIONBOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type
46 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
One corner of a long rectangular sheet of paper of width 1 unit is folded over so as to reach the opposite edge of the sheet. Find the minimum length of the crease.
View SolutionIf a leaf of a book is folded so that one corner moves along an opposite side, then prove that the line of crease will always touch parabola.
View Solution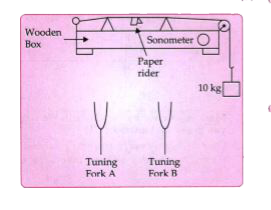
The diagram above shows a wire stretched over a sonometer. Stems of two vibrating tuning forks A and B are touched to the wooden box of the sonometer. It is observed that the paper rider (a small piece of paper folded at the centre) present on the wire flies off when the stem of vibrating tuning fork B is touched to the wooden box but the paper just vibrates when the stem of vibrating tuning fork A is touched to the wooden box.
Why does the paper rider fly off when the stem of tuning fork B is touched to the box ?
View Solution
The diagram above shows a wire stretched over a sonometer. Stems of two vibrating tuning forks A and B are touched to the wooden box of the sonometer. It is observed that the paper rider (a small piece of paper folded at the centre) present on the wire flies off when the stem of vibrating tuning fork B is touched to the wooden box but the paper just vibrates when the stem of vibrating tuning fork A is touched to the wooden box.
Name the phenomenon when the paper rider flies off.
View SolutionThe diagram below shows a wire stretched over a sonometer. Stems of two vibrating tuning forks A and B are touched in turn to the wooden box of the sonometer. It is observed that the paper rider (a small piece of paper folded at the centre) present on the wire flies off when the stem of vibrating tuning fork B is touched to the wooden box but the paper just vibrates when the stem of vibrating tuning fork A is touched to the wooden box.
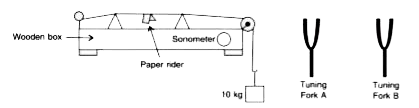
Name the phenomenon when the paper rider just vibrates.
View SolutionThe radius of the curved road on a national highway is R. The width of the road is b. The outer edge of the road is raised by h with respect to the inner edge so that a car with velocity v can pass safe over it. The value of h is
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If a clown holds on to hoop instead of passing through it, what is the position of the cable so that he doesn't hit his head on the ceiling as he swings upward?
View SolutionRead the following passage carefully and answer the questions that follow:
Attending classes inside a railway carriage seemed unusual enough, but the seating arrangements turned out to be unusual, too. At Totto-chan.s previous school each pupil was assigned a specific desk. But here they could sit anywhere they liked at any time.
The most unusual thing of all about this school, however, was the lessons themselves. Schools normally schedule one subject, for example history, during the first period, when everyone in the class just did history, then say arithmetic in the second period, when you just did arithmetic. But here it was quite different. At the beginning of the first period, the teacher made a list of all the problems and questions in the subjects to be studied that day. Then she would say, "Now, start with any of these you like".
So, whether you started on history or arithmetic or something else didn.t matter at all. Someone who liked composition might be writing something, while behind you someone who liked chemistry might be boiling something in a flask over an alcohol burner. This method of teaching enabled the teachers to observe-as the children progressed to higher grades- what they were interested in as well as their way of thinking and their character. It was an ideal way for teachers to really get to know their pupils.
As for the pupils, they loved being able to start with their favourite subject, the fact that they had all day to cope with the subjects they disliked meant they could usually manage them somehow. So, study was mostly independent, with pupils free to go and consult the teacher whenever necessary. Then pupils would be given further exercises to work at alone. It was study in the truest sense of the word, and it meant there were no pupils just sitting inattentively while the teacher talked and explained.
The first-grade pupils hadn.t quite reached the stage of independent study, but even they were allowed to start with any subject they wanted. Some copied letters of the alphabet, some drew pictures, some read books, and some even did physical exercises.
Just then the boy sitting behind her got up and walked toward the blackboard with this notebook, apparently to consult the teacher. Totto-chan stopped looking around the room and fixed her eyes on his back as he walked. The boy dragged his leg, and his whole body swayed from side to side, Totto chan wondered at first if he was doing it on purpose, but she soon realized the boy couldn.t help it.
The boy said brightly, "My name.s Yasuaki. What.s yours?" She was so glad to hear him speak that she replied loudly, "I.m Totto chan".
Give the meaning of the following words as used in the passage:
One-word answers or short phrases will be accepted.
assigned
View SolutionRead the following passage carefully and answer the questions that follow:
Attending classes inside a railway carriage seemed unusual enough, but the seating arrangements turned out to be unusual, too. At Totto-chan.s previous school each pupil was assigned a specific desk. But here they could sit anywhere they liked at any time.
The most unusual thing of all about this school, however, was the lessons themselves. Schools normally schedule one subject, for example history, during the first period, when everyone in the class just did history, then say arithmetic in the second period, when you just did arithmetic. But here it was quite different. At the beginning of the first period, the teacher made a list of all the problems and questions in the subjects to be studied that day. Then she would say, "Now, start with any of these you like".
So, whether you started on history or arithmetic or something else didn.t matter at all. Someone who liked composition might be writing something, while behind you someone who liked chemistry might be boiling something in a flask over an alcohol burner. This method of teaching enabled the teachers to observe-as the children progressed to higher grades- what they were interested in as well as their way of thinking and their character. It was an ideal way for teachers to really get to know their pupils.
As for the pupils, they loved being able to start with their favourite subject, the fact that they had all day to cope with the subjects they disliked meant they could usually manage them somehow. So, study was mostly independent, with pupils free to go and consult the teacher whenever necessary. Then pupils would be given further exercises to work at alone. It was study in the truest sense of the word, and it meant there were no pupils just sitting inattentively while the teacher talked and explained.
The first-grade pupils hadn.t quite reached the stage of independent study, but even they were allowed to start with any subject they wanted. Some copied letters of the alphabet, some drew pictures, some read books, and some even did physical exercises.
Just then the boy sitting behind her got up and walked toward the blackboard with this notebook, apparently to consult the teacher. Totto-chan stopped looking around the room and fixed her eyes on his back as he walked. The boy dragged his leg, and his whole body swayed from side to side, Totto chan wondered at first if he was doing it on purpose, but she soon realized the boy couldn.t help it.
The boy said brightly, "My name.s Yasuaki. What.s yours?" She was so glad to hear him speak that she replied loudly, "I.m Totto chan".
Give the meaning of the following words as used in the passage:
One-word answers or short phrases will be accepted.
independent
View SolutionRead the following passage carefully and answer the questions that follow:
Attending classes inside a railway carriage seemed unusual enough, but the seating arrangements turned out to be unusual, too. At Totto-chan.s previous school each pupil was assigned a specific desk. But here they could sit anywhere they liked at any time.
The most unusual thing of all about this school, however, was the lessons themselves. Schools normally schedule one subject, for example history, during the first period, when everyone in the class just did history, then say arithmetic in the second period, when you just did arithmetic. But here it was quite different. At the beginning of the first period, the teacher made a list of all the problems and questions in the subjects to be studied that day. Then she would say, "Now, start with any of these you like".
So, whether you started on history or arithmetic or something else didn.t matter at all. Someone who liked composition might be writing something, while behind you someone who liked chemistry might be boiling something in a flask over an alcohol burner. This method of teaching enabled the teachers to observe-as the children progressed to higher grades- what they were interested in as well as their way of thinking and their character. It was an ideal way for teachers to really get to know their pupils.
As for the pupils, they loved being able to start with their favourite subject, the fact that they had all day to cope with the subjects they disliked meant they could usually manage them somehow. So, study was mostly independent, with pupils free to go and consult the teacher whenever necessary. Then pupils would be given further exercises to work at alone. It was study in the truest sense of the word, and it meant there were no pupils just sitting inattentively while the teacher talked and explained.
The first-grade pupils hadn.t quite reached the stage of independent study, but even they were allowed to start with any subject they wanted. Some copied letters of the alphabet, some drew pictures, some read books, and some even did physical exercises.
Just then the boy sitting behind her got up and walked toward the blackboard with this notebook, apparently to consult the teacher. Totto-chan stopped looking around the room and fixed her eyes on his back as he walked. The boy dragged his leg, and his whole body swayed from side to side, Totto chan wondered at first if he was doing it on purpose, but she soon realized the boy couldn.t help it.
The boy said brightly, "My name.s Yasuaki. What.s yours?" She was so glad to hear him speak that she replied loudly, "I.m Totto chan".
Give the meaning of the following words as used in the passage:
One-word answers or short phrases will be accepted.
ideal
View Solution
