PandQ are two points on a circle of centre C and radius α . The angle PCQ being 2θ , find the value of sinθ when the radius of the circle inscribed in the triangle CPQ is maximum.
We know that r=△s, where
△ = Area of triangle CPQ and s= semiperameter of triangleCPQ
∴r=α2(sin2θ)2s=α2sin2θ2α+2αsinθ=α2.sin2θ1+sinθ

Now for f(θ)=sin2θ1+sinθ
f(θ)=(1+sinθ)2cos2θ−sin2θ.cosθ(1+sinθ)2
or 2(1+sinθ)(1−2sin2θ)−2sinθ(1−sin2θ)=0
or 2(1−sin2θ)=2sinθ(1−sinθ)
or 1−2sin2θ=sinθ−sin2θ
or sin2θ=sinθ−sin2θ
or sin2θ+sinθ−1=0
or sinθ=√5−12
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Concept Application Exercise 6.1
Explore 10 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Concept Application Exercise 6.2
Explore 10 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Matrix Match Type
Explore 14 Videos
- METHODS OF DIFFERENTIATIONBook:CENGAGE ENGLISHChapter:METHODS OF DIFFERENTIATIONExercise:Single Correct Answer Type
Explore 46 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSExercise:Comprehension Type
Explore 6 Videos
Similar Questions
In a right angled triangle ABC, right angled at B, BC=12cm and AB=5cm. The radius of the circle inscribed in the triangle (in cm) is :
View SolutionAn isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a . Show that the area of the triangle is maximum when θ=π6 .
View SolutionIf the tangent at a point P to a circle with centre O cuts a line through O at Q such that PQ=24cm and OQ=25cm . Find the radius of the circle.
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
View SolutionA point P is 13cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12 cm. Find the radius of the circle.
View SolutionMake a point P and draw a circle with centre P and radius 5 cm. Take any point Q on the circle drawn. With Q as centre and radius 3 cm draw another circle. Label the two points at which the circles intersect as A and B. Join PQ and AB. Find the angle between AB and PQ.
View SolutionA circle is inscribed in an equilateral triangle ABC of side 12 cm, touching its sides (Figure). Find the radius of the inscribed circle and the area of the shaded part.
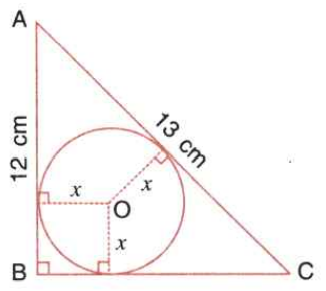
View SolutionABC is a right angled triangle with AB=12 cm and AC=13 cm. A circle, with centre O has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.
View SolutionDraw a circle of radius 3 cm. Take a point P outside it. Without using the centre of the circle, draw two tangents to the circle from the point P.
View SolutionDraw a circle of radius 3 cm and take a point P outside it. Without using the centre of the circle draw two tangents of the circle from the point P.
View Solution

