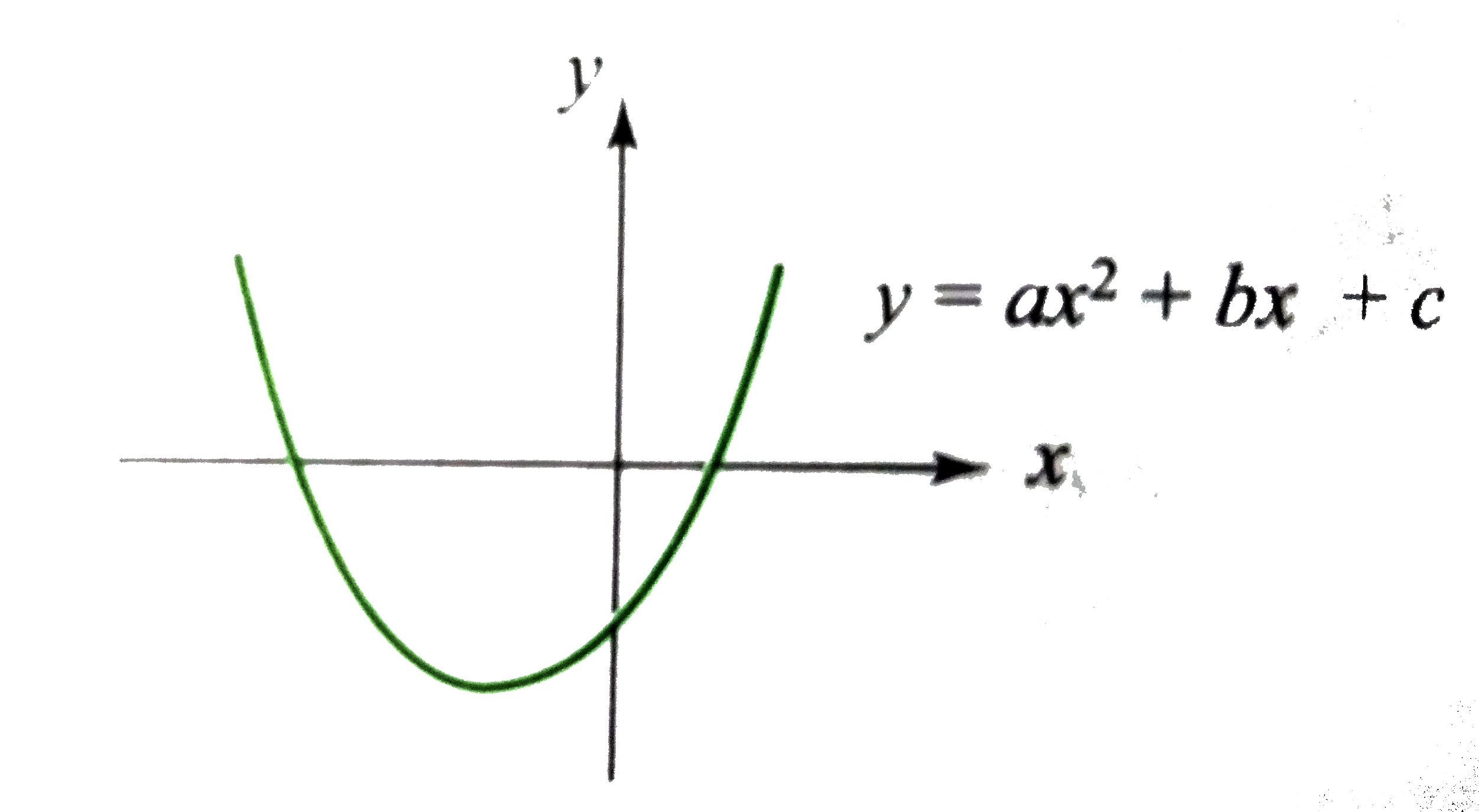
Let f(X)=ax2+bx+c. Consider the following diagram
 .
.
c<0
b>0
a+b−c>0
abc<0
The correct Answer is:1,2,3,4
Let f(x)=ax2+bx+c
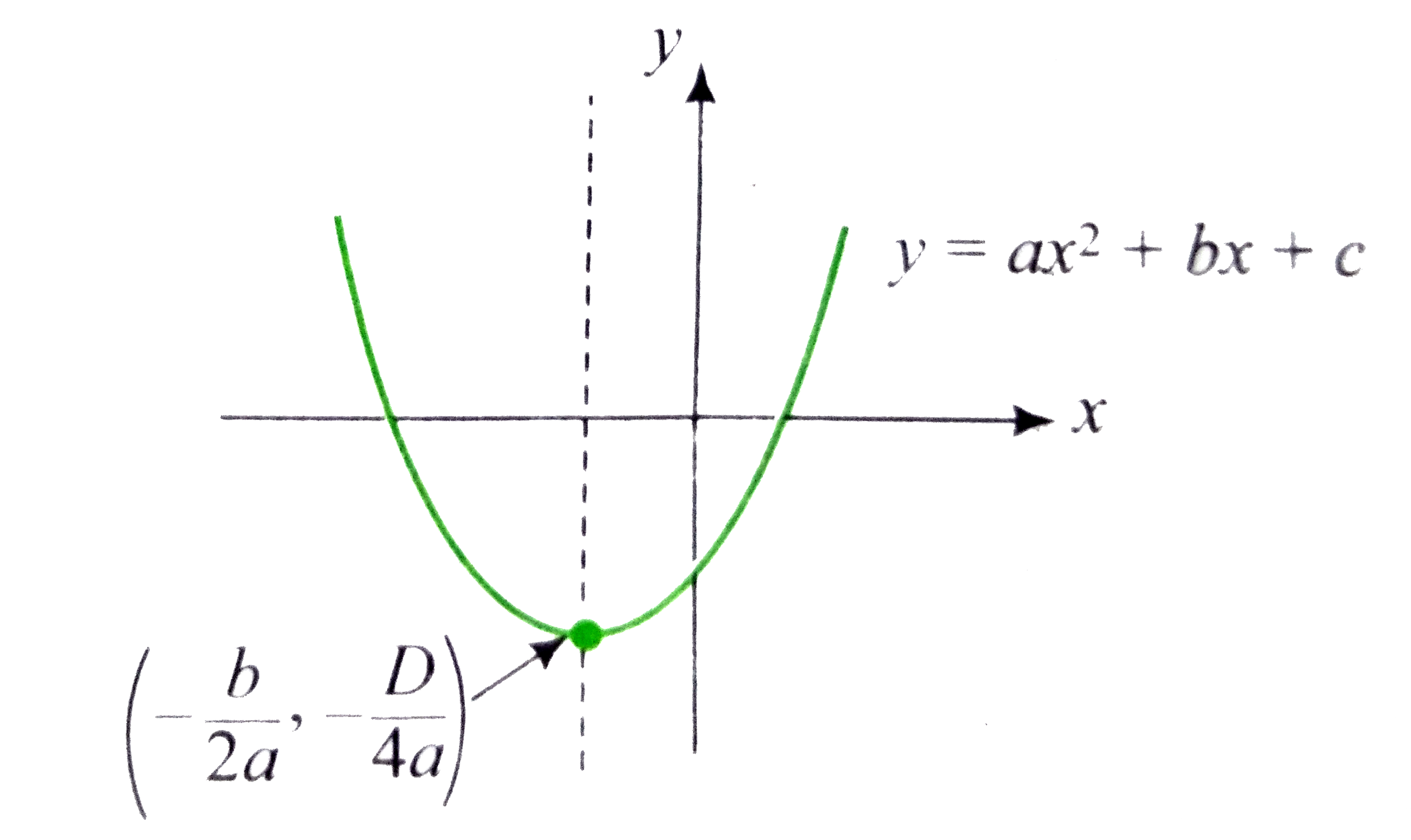
For the diagram, we can see that a>0,c<0and−[b(2a)]<0 .
Hence , b>0
∴a+b−c>0
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Linked Comprechension Type
37 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - MATRIX MATCH TYPE
6 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Single Correct Answer Type : Exercise
89 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
Let f(x)=ax2+bx+⋅ Consider the following diagram. Then Fig c<0 b>0 a+b−c>0 abc<0
View Solution(iv) Let y=1ax2+bx+c then find dy/dx
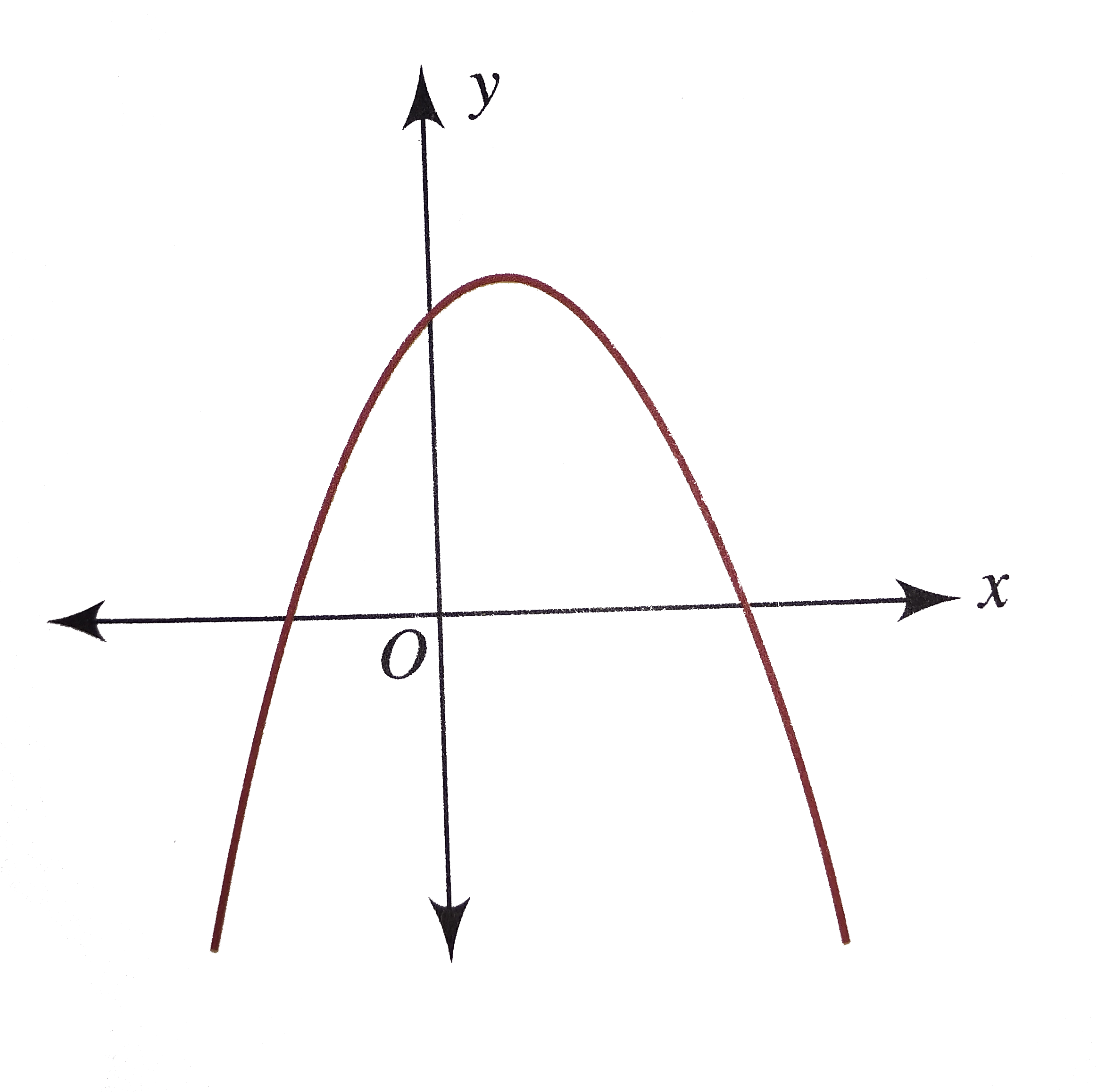
View SolutionThe following figure shows the graph of f(x)=ax2+bx+c, find the signs of a,bandc.
View SolutionConsider that f:R→R
(i) Let f(x)=x3+x2+ax+4 be bijective, then find a.
(ii) Let f(x)=x3+bx2+cx+d is bijective, then find the condition.
View SolutionLet f(x)=ax2+bx+c,a,b,c,∈R and equation f(x)−x=0 has imaginary roots α,β. If r, s be the roots of f(f(x))−x=0, then ∣∣ ∣ ∣∣2αδβ0αγβ1∣∣ ∣ ∣∣ is
View SolutionConsider that f(x)=ax2+bx+c,D=b2−4ac , then which of the following is not true ?
View SolutionLet f(x)=ax2−bx+c2,b≠0andf(x)≠0 for all x∈R. Then
View SolutionThe following figure shows the graph of f(x)=ax2+bx+c, then find the sign of values of a,bandc.
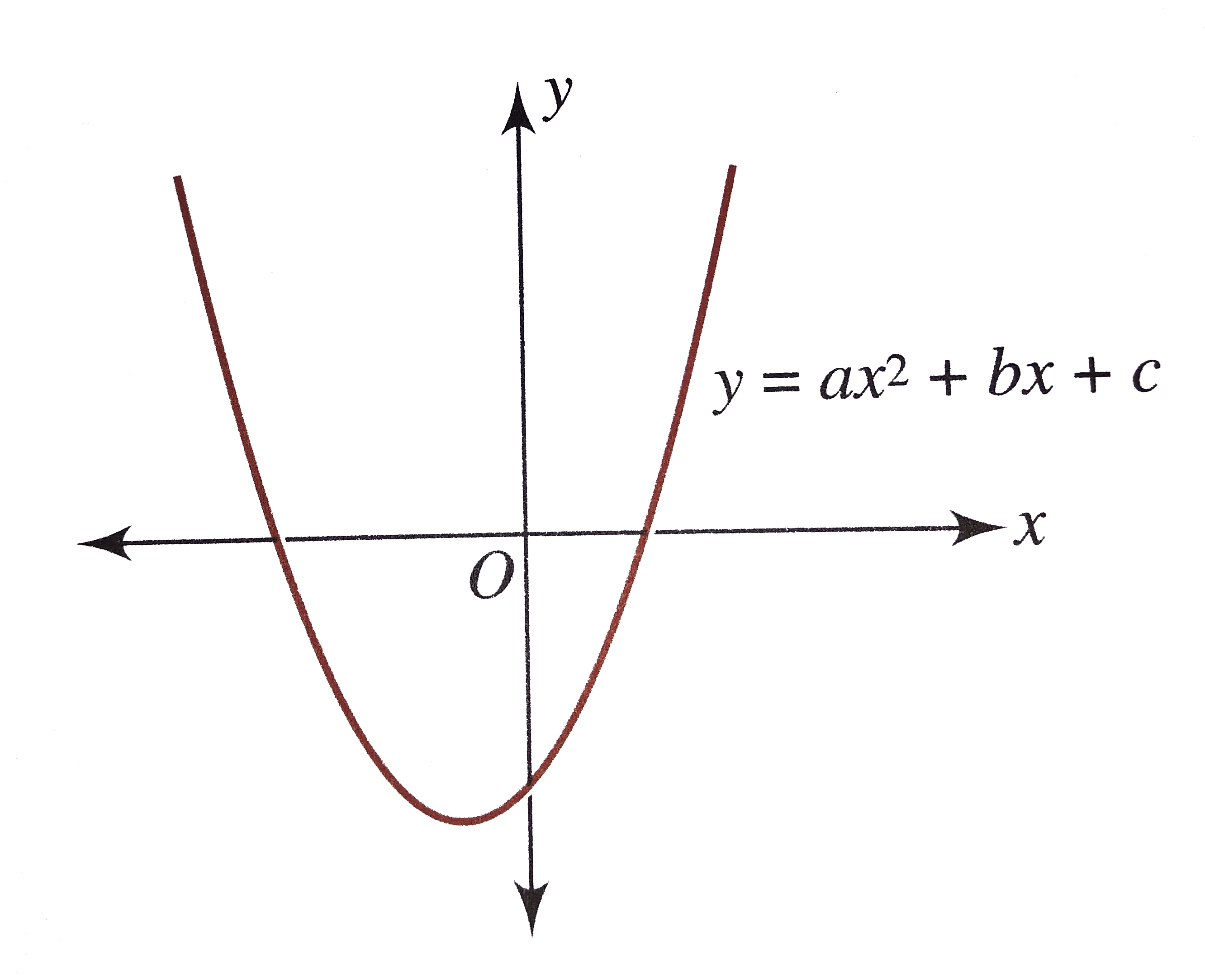
View SolutionLet f(x)=ax3+bx2+cx+dsinx. Find the condition that f(x) is always one-one function.
View SolutionLet f(x)=ax2+bx+c and f(−1)<1,f(1)>−1,f(3)<−4 and a≠0, then
View Solution
