(iv) Let y=1ax2+bx+c then find dy/dx
The correct Answer is:=−(2ax+b)(ax2+bx+c)2
To find the derivative of the function y=1ax2+bx+c, we will use the chain rule and the power rule of differentiation. Here’s the step-by-step solution:
Step 1: Rewrite the function
We can rewrite the function y in a form that is easier to differentiate:
y=(ax2+bx+c)−1
Step 2: Differentiate using the chain rule
Now, we will differentiate y with respect to x. Using the chain rule, we have:
dydx=−1⋅(ax2+bx+c)−2⋅ddx(ax2+bx+c)
Step 3: Differentiate the inner function
Next, we need to find the derivative of the inner function ax2+bx+c:
ddx(ax2+bx+c)=2ax+b
Step 4: Substitute back into the derivative
Now, substituting this back into our expression for dydx:
dydx=−1⋅(ax2+bx+c)−2⋅(2ax+b)
Step 5: Simplify the expression
Thus, we can write:
dydx=−2ax+b(ax2+bx+c)2
Final Answer
The derivative of y with respect to x is:
dydx=−2ax+b(ax2+bx+c)2
---
We can rewrite the function y in a form that is easier to differentiate:
y=(ax2+bx+c)−1
Now, we will differentiate y with respect to x. Using the chain rule, we have:
dydx=−1⋅(ax2+bx+c)−2⋅ddx(ax2+bx+c)
Next, we need to find the derivative of the inner function ax2+bx+c:
ddx(ax2+bx+c)=2ax+b
Now, substituting this back into our expression for dydx:
dydx=−1⋅(ax2+bx+c)−2⋅(2ax+b)
Thus, we can write:
dydx=−2ax+b(ax2+bx+c)2
The derivative of y with respect to x is:
dydx=−2ax+b(ax2+bx+c)2
Topper's Solved these Questions
- DIFFERENTIATIONBOOK - ICSECHAPTER - DIFFERENTIATIONEXERCISE - EXERCISE 19 (a)
12 Videos
- DIFFERENTIATIONBOOK - ICSECHAPTER - DIFFERENTIATIONEXERCISE - EXERCISE 19 (b)
26 Videos
- CORRELATION ANALYSISBOOK - ICSECHAPTER - CORRELATION ANALYSISEXERCISE - Multiple Choice Question
7 Videos
- ELLIPSEBOOK - ICSECHAPTER - ELLIPSEEXERCISE - CHAPTER TEST
10 Videos
Similar Questions
(ii) Let y=xa2+x2 then find dy/dx
View Solution(i) Let y=(2+5x)2x3−1 then find dy/dx
View SolutionIf y=1√x=(x)−1/2, then find dy/dx.
View SolutionIf y=(ax+b)(x2+c) , then find dydx .
View SolutionIf y2=ax2+bx+c , then find (dy)/(dx)
View SolutionIf y=[x2+1x+1], then find dydx.
View Solutiony=11+xfind dydx
View SolutionIf xy=c2 , find dydx
View SolutionIf y=[3x+2][2x−1], then find dydx.
View SolutionLet f(X)=ax2+bx+c. Consider the following diagram
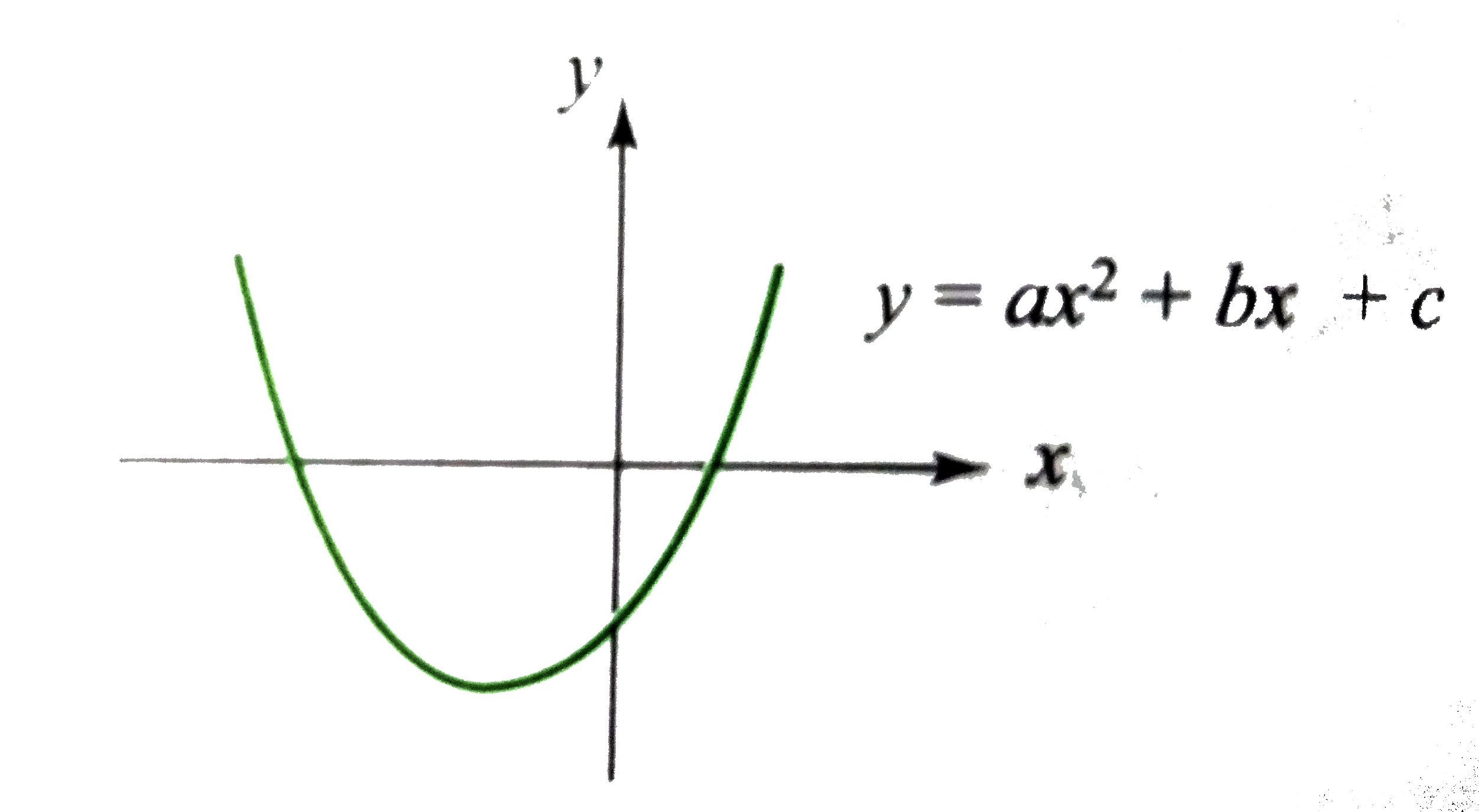 .
.
View Solution
