If x2+2ax+a<0∀x∈[1,2], the find the values of a.
Video Solution
Text Solution
Given ,
x2+2ax+a<0.∀x∈ [1, 2]
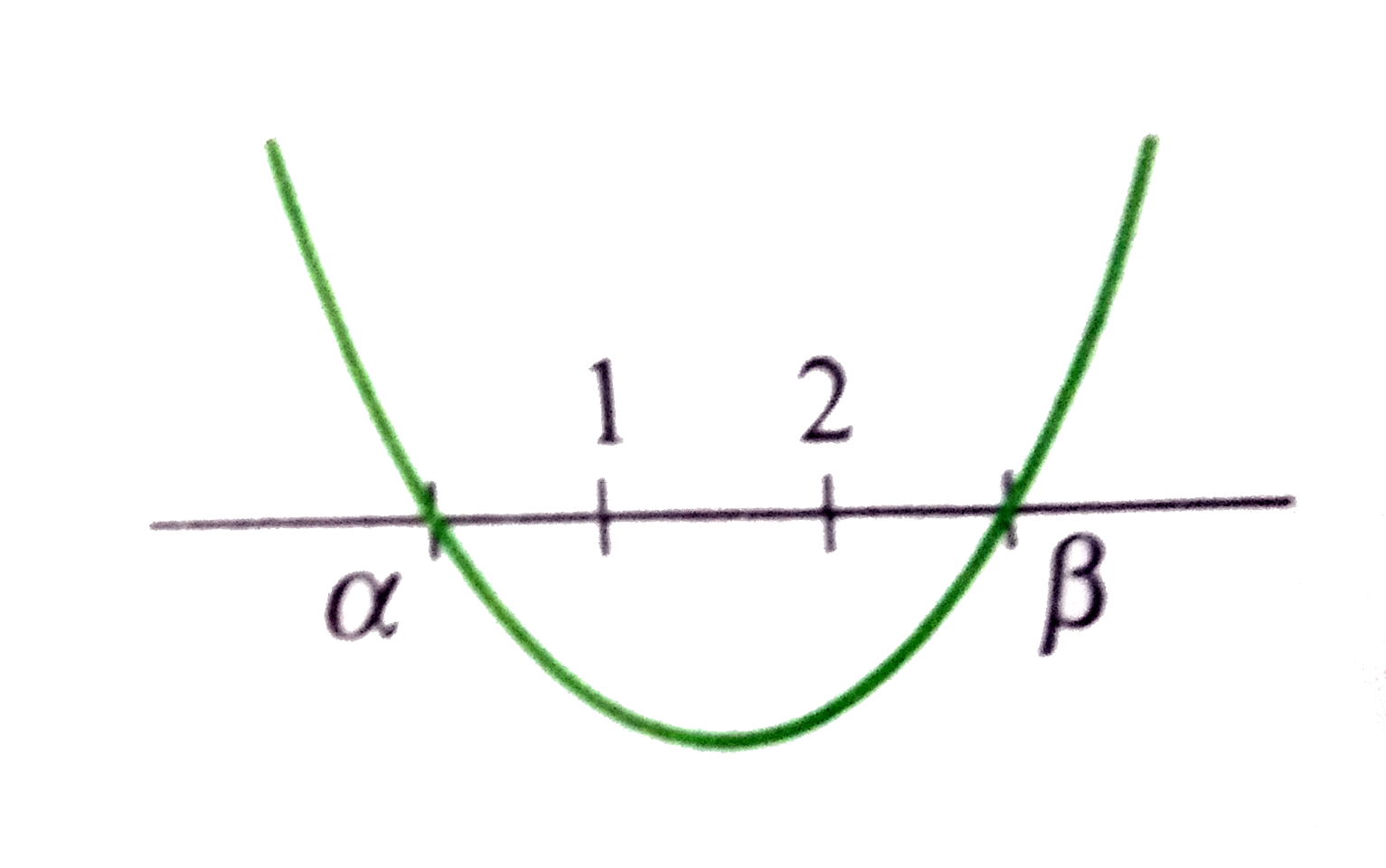
Hence, 1 and 2 lie between the roots of the equation
x2+2ax+a=0
⇒f(1)<0andf(2)<0
⇒1+2a+a<0,4+4a+a<0
⇒a<−13,a<−45
⇒a∈(−∞,−45)
|
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - SOLVED EXAMPLES
14 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.1
3 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer
6 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
Knowledge Check
If (x - 2), (x + 2), (2x + 1) and (2x + 19) are in proportion, then the value of x is ...............
A5B6C3D4
If f(x) = x2−2x+4x2+2x+4,x∈R then range of function is
View SolutionIf x = 3, what is the sum of 2x(2x+1),(2x+2),(2x+3), and (2x+4)?
View SolutionLet f(x)=x+√x2+2xandg(x)=√x2+2x−x, then:
View SolutionSolve: ∣∣ ∣ ∣∣x2−1x2+2x+12x2+3x+12x2+x−12x2+5x−32x2+4x−36x2−x−26x2−7x+212x2−5x−2∣∣ ∣ ∣∣=0.
View SolutionIf ∣∣ ∣∣x−42x2x2xx−42x2x2xx−4∣∣ ∣∣=(A+Bx)(x−A)2 then the ordered pair (A,B) is equal to
View SolutionIf f(x)=⎧⎨⎩(x−2)2−(1|x−2|+1x−2)x≠20x=2 then f(x) at x=2 is
View SolutionSimplify (4x2+2x2−3(x−7)−(−2x4−2x2+3x−5))
View Solution
