Find the value of a for which ax2+(a−3)x+1<0 for at least one positive real x.
Let f(x)=ax2+(a−3)x+1
Case I:
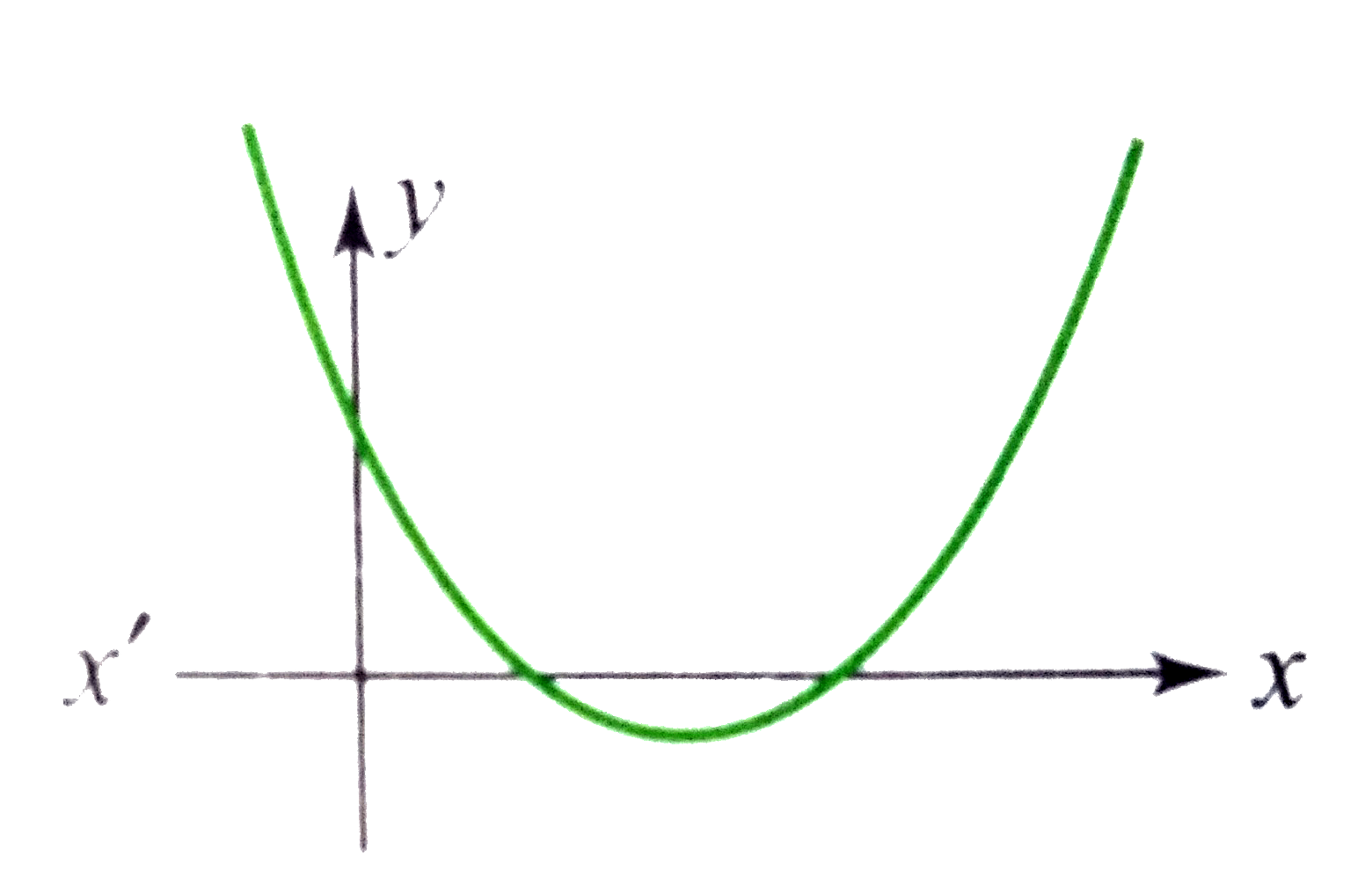
If a > 0, then f(x) will be negative only for those value of x which lie between the roots . From the graphs, we can see that f(x) will be less then zero for at least one positive real x, when f (x) = 0 has distinct roots and at least one of these roots is positive.
Since f(0) = 1 > 0, the possible grapha according to the question is shown in the figure. From the graph, we can see that both the roots are non-negative . For this
(i) D>0⇒(a−3)2−4a>0
⇒a<1ora>9 (1)
(ii) sum >0 and product ≥0
⇒−(a−3)a>0ora−3a<0and1/a>0
⇒0<a<3 (2)
From (1) and (2), we have
a ∈(0,1)
Case II : a <0
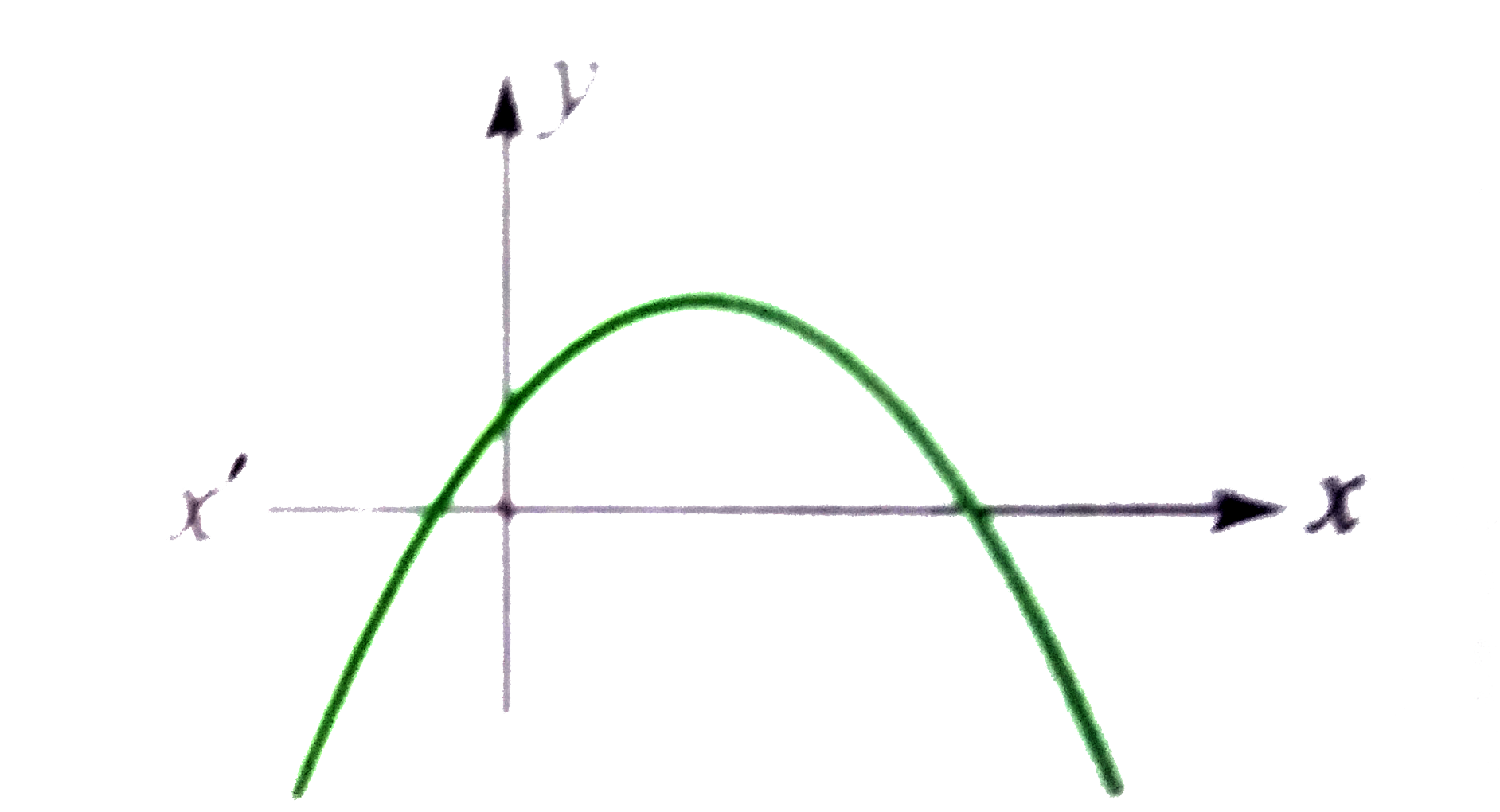
Since f(0)=1>0, then graph is as shown in the figure, which shows that ax2+(a−3)x+1< 0, for at least one positive x .
Case III : a = 0
If a = 0,
f(x) = - 3x + 1
⇒f(x)<0,∀x>1/3
Thus, from all the cases, the required set of values of a is (−∞,1) .
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - SOLVED EXAMPLES
14 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.1
3 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer
6 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
Find the values of k for which
(k+1)x2−2(3k+1)x+8k+1=0
has real and equal roots.
View SolutionFind the values of 'a' for which −3<x2+ax−2x2+x+1<2 is valid for all real x.
View SolutionFind the value of x for which f(x)=2sin−1√1−x+sin−1(2√x−x2) is constant
View SolutionFind the values of x for which matrix ⎡⎢⎣3−1+x23−1x+2x+3−12⎤⎥⎦ is singular.
View SolutionFind the set of values of x for which tan3x−tan2x1+tan3xtan2x = 1
View SolutionFind the values of k for which ∣∣∣x2+kx+1x2+x+1∣∣∣<2,∀x∈R
View SolutionFind the value of a for which the function (a+2)x3−3ax2+9ax−1 decreases montonically for all real x.
View Solutionfind the value of x for which
f(x)=(2x−1)(x−1)2(x−2)2(x−4)2≥0.
View SolutionFind the value of x for which (x+2),2x(2x+3) are three consecutive terms of A.P.
View SolutionFind the number of integral values of 'a' for which ax2−(3a+2)x+2(a+1)<0,a≠0 holds exactly four integral value of x.
View Solution
