If ∣∣x2−2x+2∣∣−∣∣2x2−5x+2∣∣=∣∣x2−3x∣∣ then the set of values of x is
(−∞,0]∪[3,00)
[0,12]∪[2,3]
(−∞,0]∪[12,2]∪[3,∞)
[0,2]∪[3,∞)
The correct Answer is:B
To solve the equation |x2−2x+2|−|2x2−5x+2|=|x2−3x|, we will follow these steps:
Step 1: Rewrite the equation
We start by rewriting the equation:
|x2−2x+2|=|2x2−5x+2|+|x2−3x|
Step 2: Analyze the expressions inside the absolute values
Next, we need to analyze the expressions inside the absolute values. We will find the roots of each quadratic expression to determine the intervals where they change sign.
1. For x2−2x+2:
- The discriminant D=(−2)2−4⋅1⋅2=4−8=−4 (no real roots).
- This expression is always positive since it opens upwards.
2. For 2x2−5x+2:
- The discriminant D=(−5)2−4⋅2⋅2=25−16=9.
- Roots: x=5±34⇒x=2 and x=12.
3. For x2−3x:
- The roots are x(x−3)=0 giving x=0 and x=3.
Step 3: Determine intervals
The critical points are 0,12,2,3. We will analyze the sign of the expressions in the intervals:
- (−∞,0)
- (0,12)
- (12,2)
- (2,3)
- (3,∞)
Step 4: Test each interval
1. Interval (−∞,0):
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=−(2x2−5x+2)
- |x2−3x|=−(x2−3x)
2. Interval (0,12):
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=−(2x2−5x+2)
- |x2−3x|=−(x2−3x)
3. Interval (12,2):
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=2x2−5x+2
- |x2−3x|=−(x2−3x)
4. Interval (2,3):
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=2x2−5x+2
- |x2−3x|=x2−3x
5. Interval (3,∞):
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=2x2−5x+2
- |x2−3x|=x2−3x
Step 5: Solve inequalities
For each interval, we will set up inequalities based on the signs of the expressions and solve them.
Step 6: Combine solutions
After solving all the inequalities, we will combine the solutions to find the set of values of x.
Final Result
The solution set is:
x∈(0,12)∪(2,3)
We start by rewriting the equation:
|x2−2x+2|=|2x2−5x+2|+|x2−3x|
Next, we need to analyze the expressions inside the absolute values. We will find the roots of each quadratic expression to determine the intervals where they change sign.
- The discriminant D=(−2)2−4⋅1⋅2=4−8=−4 (no real roots).
- This expression is always positive since it opens upwards.
- The discriminant D=(−5)2−4⋅2⋅2=25−16=9.
- Roots: x=5±34⇒x=2 and x=12.
- The roots are x(x−3)=0 giving x=0 and x=3.
The critical points are 0,12,2,3. We will analyze the sign of the expressions in the intervals:
- (−∞,0)
- (0,12)
- (12,2)
- (2,3)
- (3,∞)
1. Interval (−∞,0):
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=−(2x2−5x+2)
- |x2−3x|=−(x2−3x)
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=−(2x2−5x+2)
- |x2−3x|=−(x2−3x)
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=2x2−5x+2
- |x2−3x|=−(x2−3x)
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=2x2−5x+2
- |x2−3x|=x2−3x
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=2x2−5x+2
- |x2−3x|=x2−3x
For each interval, we will set up inequalities based on the signs of the expressions and solve them.
After solving all the inequalities, we will combine the solutions to find the set of values of x.
The solution set is:
x∈(0,12)∪(2,3)
Topper's Solved these Questions
- SET THEORY AND REAL NUMBER SYSTEM BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Archives
1 Videos
- SET THEORY AND REAL NUMBER SYSTEM BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Concept Application Exercise 1.5
12 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
- SOLUTIONS AND PROPERTIES OF TRIANGLE BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type
6 Videos
Similar Questions
Knowledge Check
A teacher wrote the following polynomial on the board :
2x3−3x2+4x+7,x3−19x−30,2x2+5x+2,3x+2,4x2,2x2−5x+p,2x2+5x+q
Now she asked following questions to the students
If 2 x + 1 is a factors of 2x2−5x+p then the value of p isA3B6C−6D−3If −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
A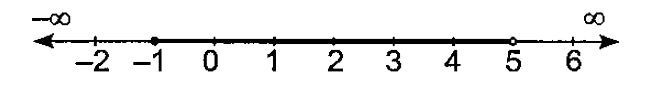 B
B C
C D
D
Let f(x)={3x2−2x+10x<1−2x>1
The set of values of b for which f(x) has greatest value at x=1 is
View SolutionLet f(x)=⎧⎪⎨⎪⎩x3−x2+10x−5,x≤1−2x+log2(b2−2),x>1. The set of values of b for which f(x) has greatest value at x= 1 is given by .
View SolutionIf |A| = 2 and A=∣∣∣2x65x1∣∣∣ then find the value of x
View SolutionIf 3x+22x≥5x, then the solution set for x, is
View SolutionLet f(x)={2−∣∣x2+5x+6∣∣x≠−2b2+1x=−2
Has relative maximum at x=−2, then complete set of values b can take is:
View SolutionLet A=⎡⎢⎣3x216x⎤⎥⎦,B=[a,b,c]and C=⎡⎢ ⎢⎣(x+2)25x22x5x22x(x+2)22x(x+2)25x2⎤⎥ ⎥⎦ be three given matrices, where a,b,candx∈R. Given that tr(AB)=tr(C). If f(x)=ax2+bx+c, then the value of f(1) is ______.
View Solution
