The solution set of the inequlity $\frac{| x - 2 | - x}{x} < 2$ is

A

(0,1)

B

[0,2]

C

$(- \infty, 0) \cup (1, \infty)$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

We have $\frac{| x + 2 | - x}{x} < 2$
$\Rightarrow \frac{| x + 2 | - 3 x}{x} < 0$
Let $| x + 2 | - 3 x = 0$
$\Rightarrow x + 2 = \pm 3 x$
$\Rightarrow x = 1$
sign scheme of the expression $\frac{| x + 2 | - 3 x}{x}$ is as shown in the following figure :

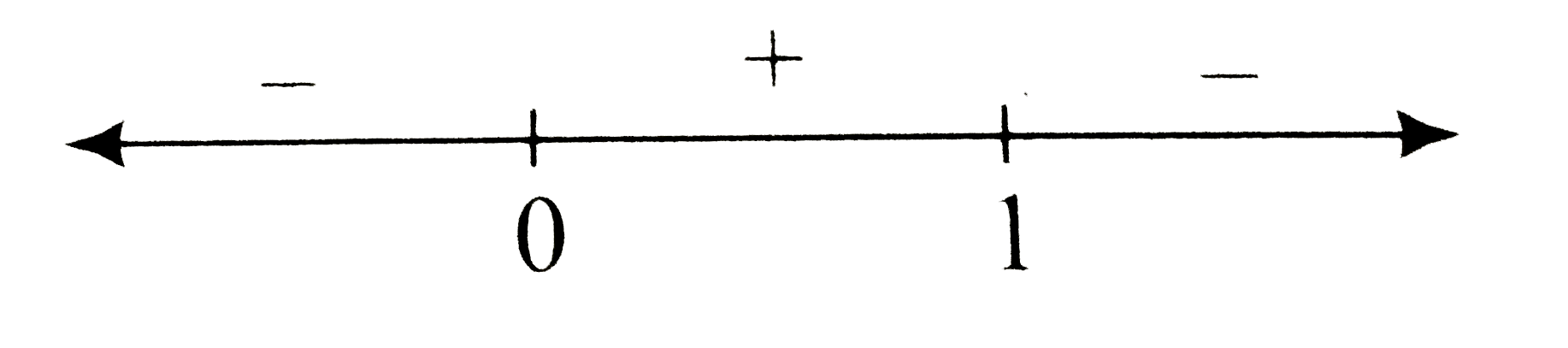
From the sing scheme $x \in (- \infty, 0) \cup (1, \infty)$

Updated on:21/07/2023

|

Class 12 MATHS SET THEORY AND REAL NUMBER SYSTEM

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-SET THEORY AND REAL NUMBER SYSTEM -EXERCISES

Home
Ask Doubt
Profile