ABC is a right angled triangle of which A is the right angle, BD is drawn perpendicular to BC meets CA produced in D. If AB = 12, AC = 16, BC = 20, then BD =
15
25
10
225
The correct Answer is:A
To solve the problem, we will use the properties of right-angled triangles and the concept of similar triangles.
1. Identify the Triangle and Given Values:
- We have a right-angled triangle ABC where angle A is the right angle.
- The lengths of the sides are given as:
- AB = 12
- AC = 16
- BC = 20
2. Understanding the Geometry:
- BD is drawn perpendicular to BC and meets CA produced at point D.
- We need to find the length of BD.
3. Using Trigonometric Ratios:
- Let angle θ be the angle at B in triangle BDC.
- In triangle BDC, we can express the tangent of angle θ as:
tan(θ)=BDBC=BD20
4. Finding the Angle θ in Triangle ABC:
- In triangle ABC, we can also express the tangent of angle θ as:
tan(θ)=ABAC=1216=34
5. Setting the Equations Equal:
- Since both expressions represent tan(θ), we can set them equal to each other:
BD20=34
6. Solving for BD:
- Cross-multiplying gives us:
4⋅BD=3⋅20
4⋅BD=60
BD=604=15
7. Conclusion:
- The length of BD is 15 units.
Final Answer:
BD = 15 units.
- We have a right-angled triangle ABC where angle A is the right angle.
- The lengths of the sides are given as:
- AB = 12
- AC = 16
- BC = 20
- BD is drawn perpendicular to BC and meets CA produced at point D.
- We need to find the length of BD.
- Let angle θ be the angle at B in triangle BDC.
- In triangle BDC, we can express the tangent of angle θ as:
tan(θ)=BDBC=BD20
- In triangle ABC, we can also express the tangent of angle θ as:
tan(θ)=ABAC=1216=34
- Since both expressions represent tan(θ), we can set them equal to each other:
BD20=34
- Cross-multiplying gives us:
4⋅BD=3⋅20
4⋅BD=60
BD=604=15
- The length of BD is 15 units.
BD = 15 units.
Topper's Solved these Questions
- SOLUTIONS AND PROPERTIES OF TRIANGLE Book:CENGAGE ENGLISHChapter:SOLUTIONS AND PROPERTIES OF TRIANGLE Exercise:Multiple Correct Answers Type
Explore 13 Videos
- SOLUTIONS AND PROPERTIES OF TRIANGLE Book:CENGAGE ENGLISHChapter:SOLUTIONS AND PROPERTIES OF TRIANGLE Exercise:Comprehension Type
Explore 6 Videos
- SET THEORY AND REAL NUMBER SYSTEM Book:CENGAGE ENGLISHChapter:SET THEORY AND REAL NUMBER SYSTEM Exercise:Archives
Explore 1 Video
- STATISTICSBook:CENGAGE ENGLISHChapter:STATISTICSExercise:Archives
Explore 10 Videos
Similar Questions
Knowledge Check
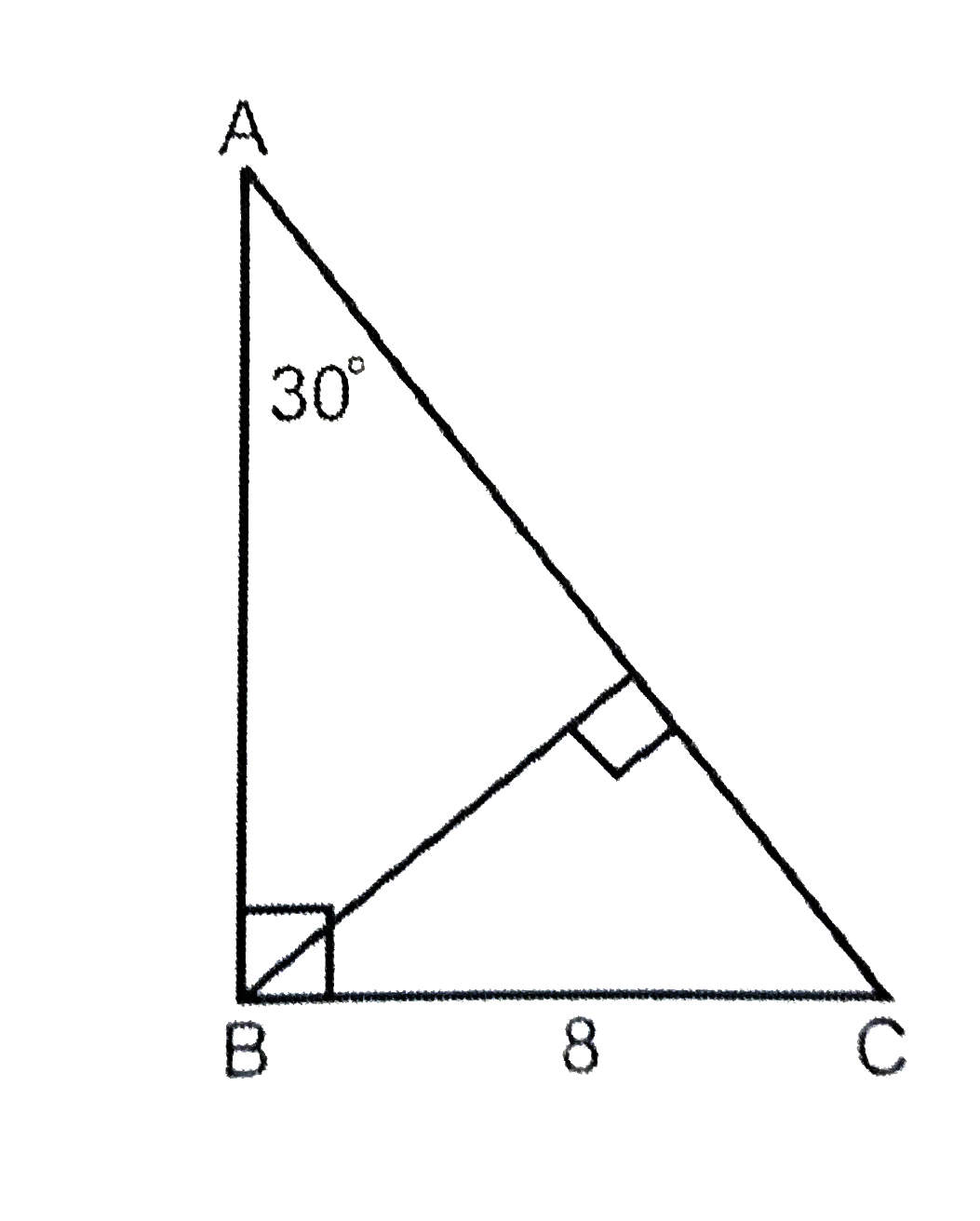
In the figure shown, ABC is a triangle, right angled at B. Through B, a line is drawn perpendicular to AC which meets AC in D. What is the length of BD?A4√3B8√3C2√3D4√3
ABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

ΔADE~ΔACB.
View SolutionABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC.
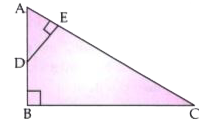
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionABC is a right-angled triangle with the right angle at vertex B. BD is the altitude through B. Given BD = 12 cm and AD = 9 cm.
Find AC.
View SolutionABC is a right-angled triangle with the right angle at vertex B. BD is the altitude through B. Given BD = 12 cm and AD = 9 cm.
Calculate AB .
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

Find, area of AADE: area of quadrilateral BCED.
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View Solution


