ABC is a right-angled triangle with the right angle at vertex B. BD is the altitude through B. Given BD = 12 cm and AD = 9 cm.
Calculate AB .
The correct Answer is:15 cm
To solve the problem, we need to find the length of side AB in triangle ABC, where BD is the altitude from vertex B to side AC. We are given that BD = 12 cm and AD = 9 cm.
1. Identify the Right Triangle:
We have triangle ABC with a right angle at B. The altitude BD divides the triangle into two smaller right triangles: ABD and BDC.
2. Apply the Pythagorean Theorem:
In triangle ABD, we can apply the Pythagorean theorem. According to the theorem:
AB2=AD2+BD2
3. Substitute the Given Values:
We know that:
- AD=9cm
- BD=12cm
Now substituting these values into the equation:
AB2=92+122
4. Calculate the Squares:
Calculate 92 and 122:
92=81
122=144
5. Add the Squares:
Now add the two results:
AB2=81+144=225
6. Find the Length of AB:
To find AB, take the square root of both sides:
AB=√225=15cm
Final Answer:
Thus, the length of AB is 15cm.
---
We have triangle ABC with a right angle at B. The altitude BD divides the triangle into two smaller right triangles: ABD and BDC.
In triangle ABD, we can apply the Pythagorean theorem. According to the theorem:
AB2=AD2+BD2
We know that:
- AD=9cm
- BD=12cm
AB2=92+122
Calculate 92 and 122:
92=81
122=144
Now add the two results:
AB2=81+144=225
To find AB, take the square root of both sides:
AB=√225=15cm
Thus, the length of AB is 15cm.
Topper's Solved these Questions
Similar Questions
ABC is a right-angled triangle with the right angle at vertex B. BD is the altitude through B. Given BD = 12 cm and AD = 9 cm.
Find AC.
View SolutionABC is a right-angled triangle with the right angle at vertex B. BD is the altitude through B.given BD=12cm and AD=9cm.
Name the triangles which are similar to triangle ADB (Proof not required).
View SolutionIn the right-angled triangle QPR, PM altitude.
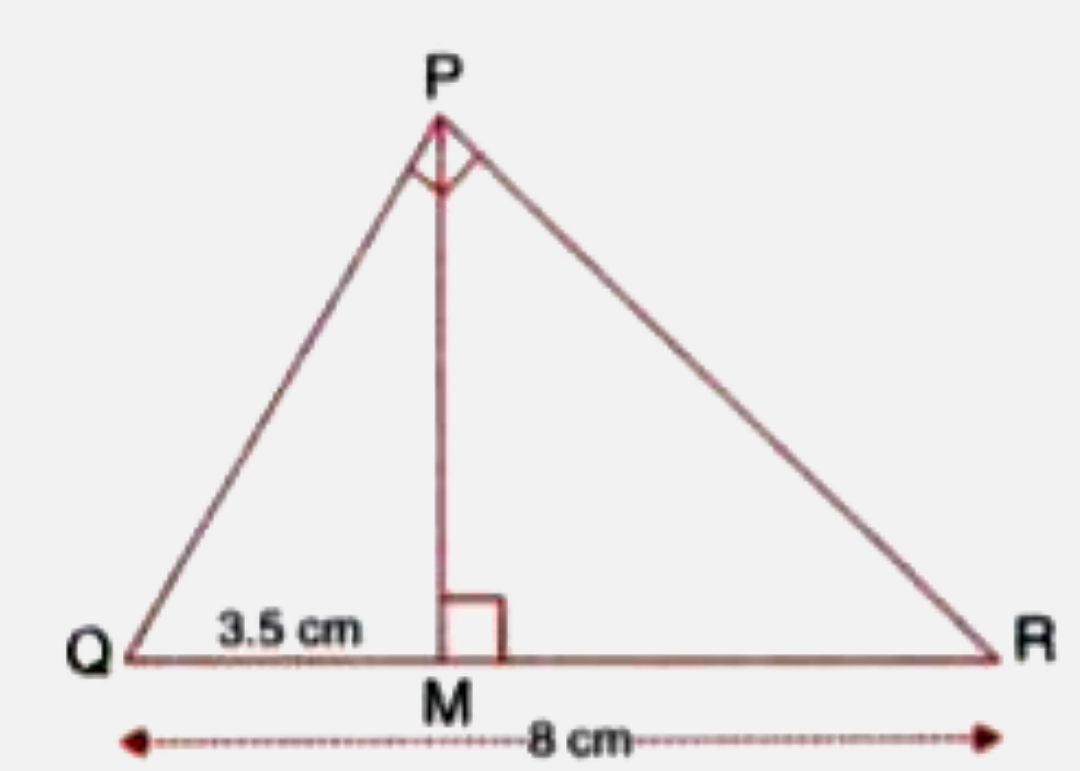
Given that QR = 8 cm and MQ = 3-5 cm, calculate the value of PR.
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionIn the adjoining figure, ABC is a triangle right-angled at vertex A and AD is altitude.
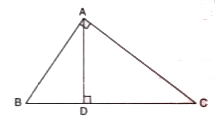
If BD = 3.6 cm and CD = 6.4 cm, find the length of AD.
View SolutionFind the ara of a right-angled triangle with hypotenuse 25 cm and altitude 24 cm.
View SolutionIf triangle ABC is right angled at C, then the value of sec (A+B) is
View SolutionIn the figure, given below, PQR is a right angled triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1:2. Calculate the lengths of PR and QR.

View SolutionABC is a right angled triangle of which A is the right angle, BD is drawn perpendicular to BC meets CA produced in D. If AB = 12, AC = 16, BC = 20, then BD =
View SolutionIn the given, figure triangle ABC is right angled at B. D is the foot of the perpendicular from B to AC. Given that BC = 3 cm and AB = 4 cm. Find :
(i) tan∠DBC
(ii) sin∠DBA
View Solution
