ABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
Step by step video & image solution for ABC is a isosceles right angled triangle, right angled at C. prove that AB^(2) = 2AC^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Revision Exercise very shot Questions
Explore 1 Video
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Revision Exercise Very Short Questions
Explore 9 Videos
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Exercise 6c
Explore 10 Videos
- STATISTICS Book:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHAN ENGLISHChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
ABC is an isosceles right triangle, right-angled at C . Prove that: AB2=2AC2.
View SolutionABC is an isosceles right triangle right-angled at C . Prove that AB2=2AC2 .
View SolutionIn figure ABC is an isosceles triangle , right angled at C . Therefore
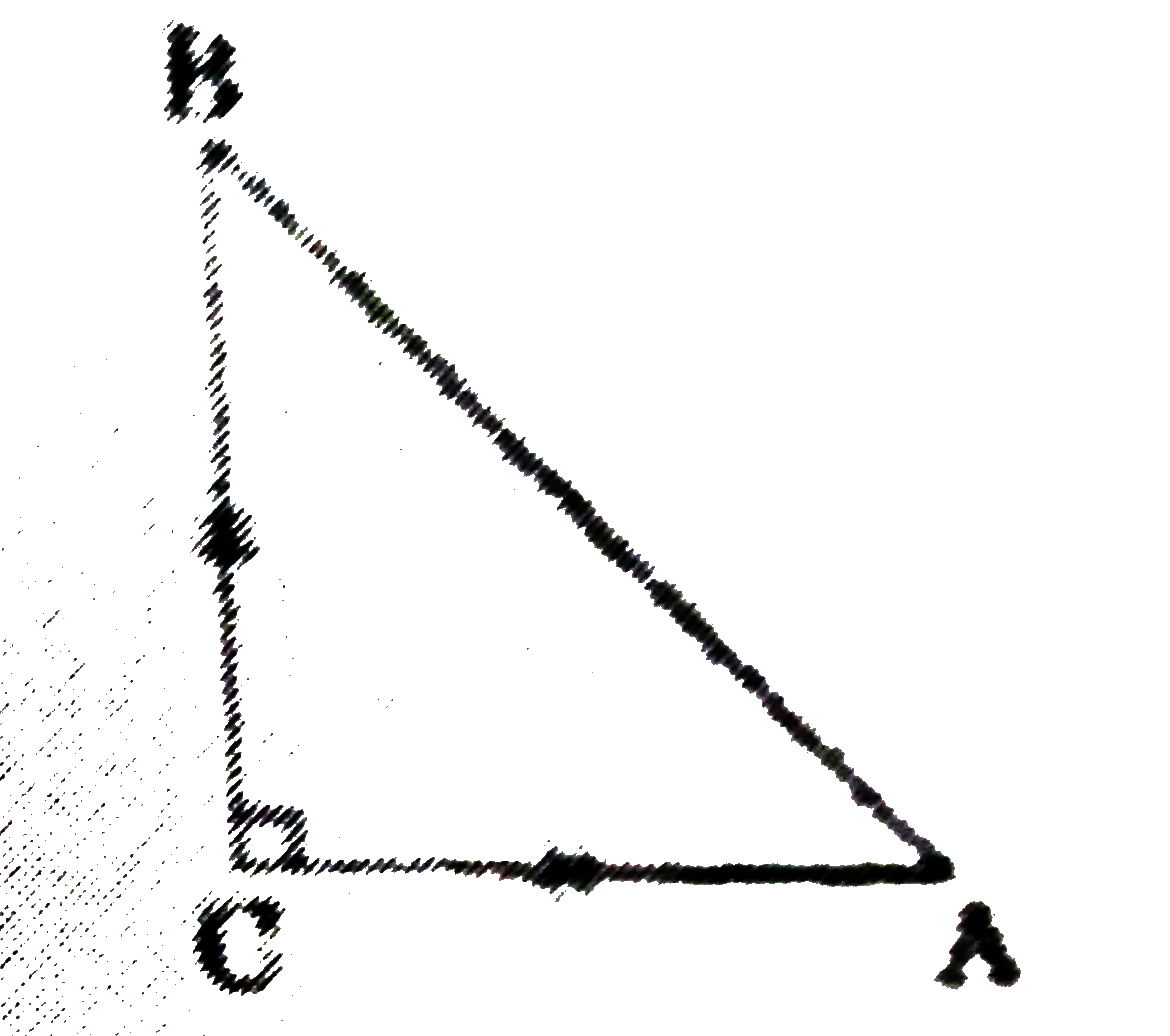
View Solutionin figure, ABC is an isosceles traingle, right angled at C. therefore
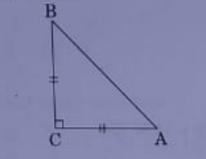
a) AB2=2AC2
b) BC2=2AB2
c) AC2=2AB2
d) AB2=4AC2
View SolutionABC is an isosceles right-triangle right angled at C such that AC=5 cm. Then, AB= (a) 2.5 cm (b) 5√2 cm (c) 10 cm (d) 5 cm
View SolutionLet the complex numbers Z1,Z2andZ3 are the vertices A, B and C respectively of an isosceles right - angled triangle ABC with right angle at C, then the value of (Z1−Z2)2(Z1−Z3)(Z3−Z2) is equal to
View SolutionΔABD is a right triangle, right-angled at A and AC⊥BD. Prove that AB2=BC×BD.
View SolutionIn Fig. 3, ABC is a right triangle, right angled at C and D is the mid-point of BC. Prove that AB2=4AD2−3AC2.
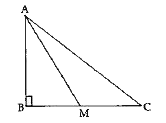
View SolutionABC is a triangle, right angled at B, M is a point on BC. Prove that :
AM2+BC2=AC2+BM2
View SolutionP and Q are the mid-points of the CA and CD respectively of a triangle ABC, right angled at C. Prove that: 4AQ2=4AC2+ BC2, 4BP2=4BC2+AC2, and 4(AQ2+ BP2)=5AB2.
View Solution

