The circle $x^{2} + y^{2} = 4$ cuts the line joining the points $A (1, 0)$ and $B (3, 4)$ in two points $P$ and $Q$ . Let $B \frac{P}{P} A = α$ and $B \frac{Q}{Q} A = β$ . Then $α$ and $β$ are roots of the quadratic equation

A

$3 x^{2} - 16 x + 21 = 0$

B

$x^{2} - 8 x + 7 = 0$

C

$x^{2} - 9 x + 8 = 0$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1

The equation of the line joining A(1,0) and B(3,4) is $y = 2 x - 2$
This cuts the circle $x^{2} + y^{2} = 4$ at $Q (0, - 2)$ and $P (8 / 5, 6 / 5)$ . We have $B Q = 3 \sqrt{5}, Q A = \sqrt{5}, B P = 7 \sqrt{5}$ and $P A = 3 \sqrt{5}$ . Therefore,
$α = \frac{B P}{P A} = \frac{7 \sqrt{5}}{3 \sqrt{5}} = \frac{7}{3}$
and $β = \frac{B Q}{Q A} = \frac{3 \sqrt{5}}{\sqrt{5}} = 3$

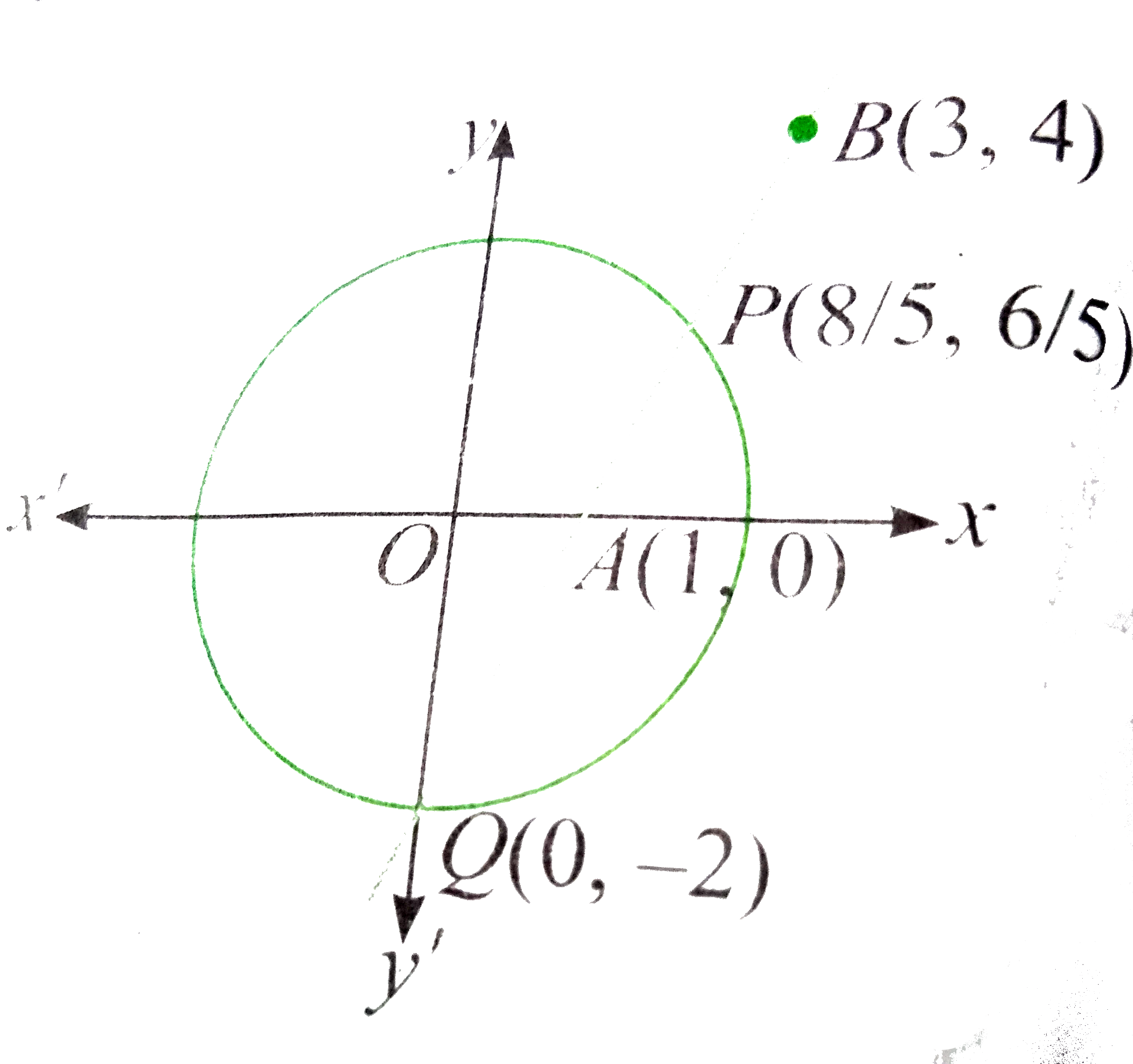
Therefore, $α$ and $β$ are roots of the equation
$x^{2} - x (a l p h + β) + α β = 0$
i.e., $x^{2} - x (\frac{7}{3} - 3) + \frac{7}{3} (3) = 0$
or $3 x^{2} - 16 x + 21 = 0$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

If $α, β$ are roots of the equation $3 x^{2} + 4 x - 5 = 0$ , then $\frac{α}{β} and \frac{β}{α}$ are roots of the equation
A $15 x^{2} + 46 x + 1 = 0$
B $15 x^{2} - 46 x + 1 = 0$
C $x^{2} + 46 x + 15 = 0$
D $x^{2} - 46 x + 15 = 0$

CENGAGE ENGLISH-CIRCLE -Excercises (Single Correct Answer Type)

Home
Ask Doubt
Profile