Question

A circle of constant radius $a$
passes through the origin $O$
and cuts the axes of coordinates at points $P$
and $Q$
. Then the equation of the locus of the foot of perpendicular from $O$
to $PQ$
is
$(x^2+y^2)(\frac{1}{x^2}+\frac{1}{y^2})=4a^2$

${(x^2+y^2)}^2(\frac{1}{x^2}+\frac{1}{y^2})=a^2$

${(x^2+y^2)}^2(\frac{1}{x^2}+\frac{1}{y^2})=4a^2$

$(x^2+y^2)(\frac{1}{x^2}+\frac{1}{y^2})=a^2$

Options

A. `(x^(2)+y^(2))((1)/(x^(2))+(1)/(y^(2)))=4a^(2)`
B. `(x^(2)+y^(2))^(2)((1)/(x^(2))+(1)/(y^(2)))=a^(2)`
C. `(x^(2)+y^(2))^(2)((1)/(x^(2))+(1)/(y^(2)))=4a^(2)`
D. `(x^(2)+y^(2))((1)/(x^(2))+(1)/(y^(2)))=a^(2)`

Answer

3

Explanation

The equation of line PQ is
`y-k=-(h)/(k)(x-h)`
or `hx+ky=h^(2)+k^(2)`
`:. Q=((h^(2)+k^(2))/(h),0)`
and `P-=(0,(h^(2)+k^(2))/(k))`
Also, `2a=sqrt(x_(1)^(2)+y_(1)^(2))`
or `x_(1)^(2)+y_(1)^(2)=4a^(2)`

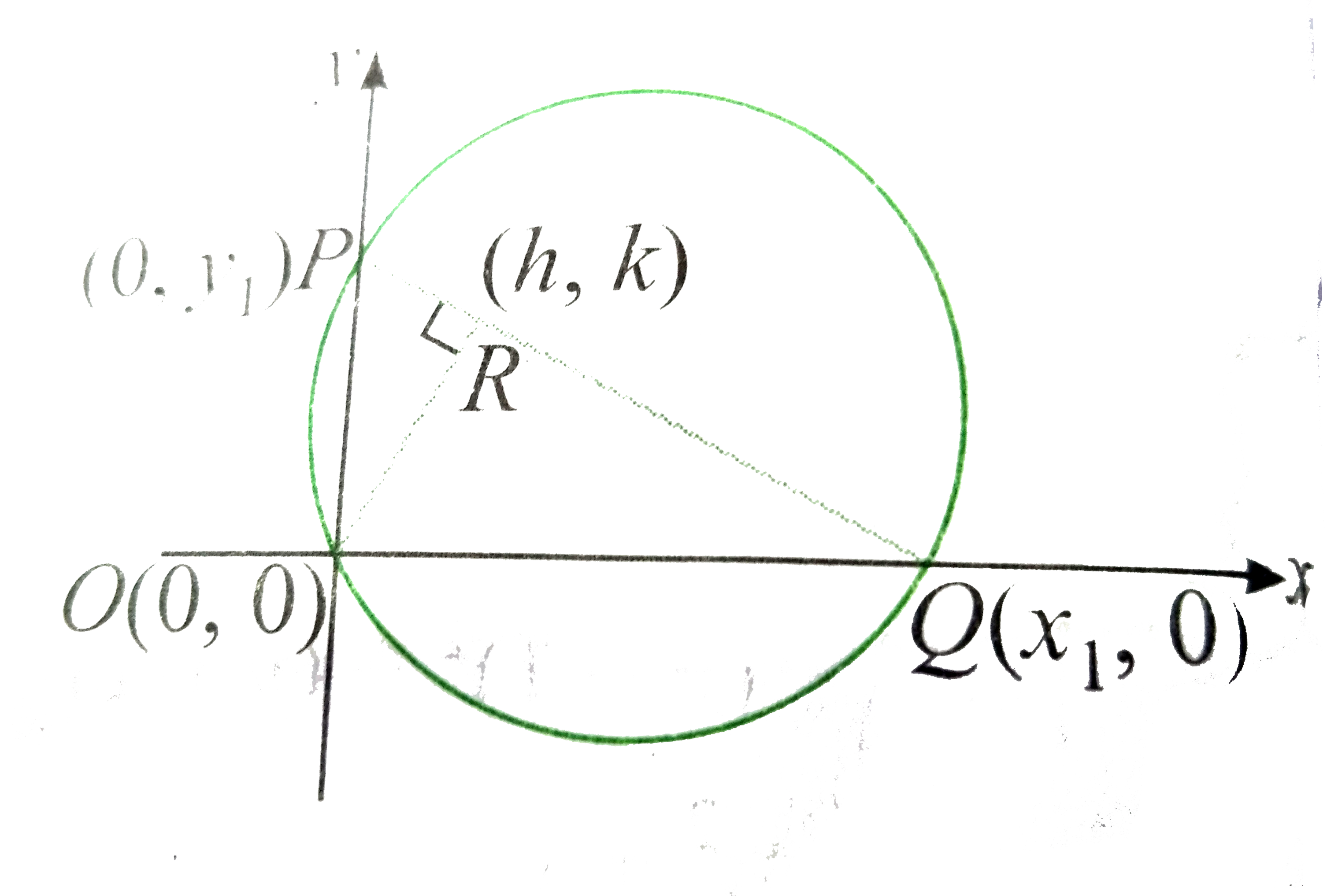
Eliminating `x_(1)` and `y_(1)`, we have
`(x^(2)+y^(2))((1)/(x^(2))+(1)/(y^(2)))=4a^(2)`