A circle is inscribed into a rhombous ABCD with one angle 60. The distance from the centre of the circle to the nearest vertex is equal to 1. If P is any point of the circle then ${| P A |}^{2} + {| P B |}^{2} + {| P C |}^{2} + {| P D |}^{2}$ is equal to:

A

12

B

11

C

9

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2

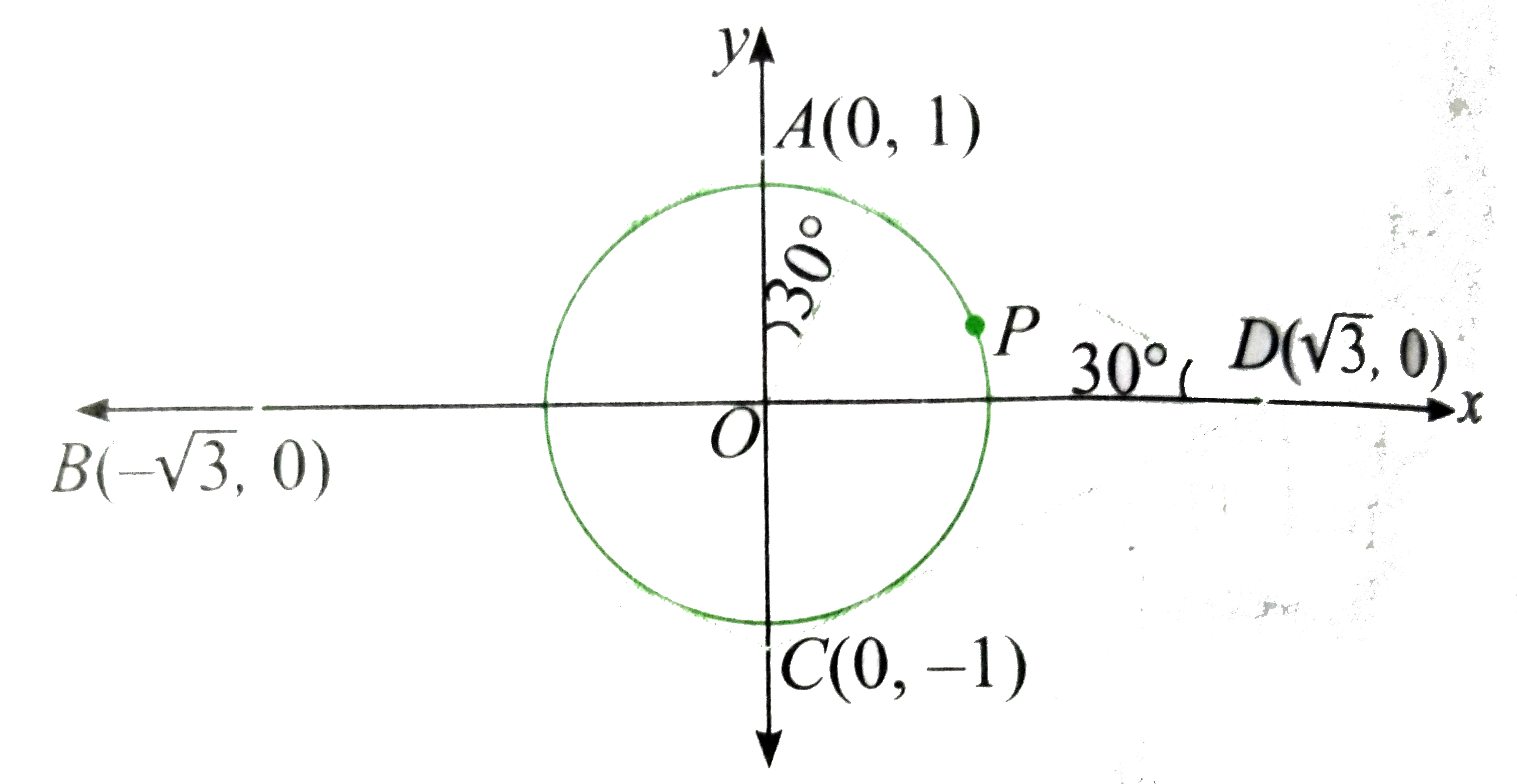
$O A = 1$
$r = O A {cos 30}^{\circ} = \frac{\sqrt{3}}{2}$
The equation of circle is
$x^{2} + y^{2} = \frac{3}{4}$
Let $P \equiv (x_{1}, y_{2})$ .
$P A^{2} + P B^{2} + P C^{2} + P D^{2} = x_{1}^{2} + {(y_{1} - 1)}_{1}^{2} + {(x_{1} + \sqrt{3})}_{1}^{2} + y_{1}^{2} + x_{1}^{2} + {(y_{1} + 1)}_{1}^{2} + {(x_{1} - \sqrt{3})}_{1}^{2} + y_{1}^{2}$
$= 4 x_{1}^{2} + 4 y_{1}^{2} + 8 = 4 (x_{1}^{2} + y_{1}^{2}) + 8$
$= 4 \times \frac{3}{4} + 8 = 11$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-CIRCLE -Excercises (Single Correct Answer Type)

Home
Ask Doubt
Profile