In triangle ABC , the equation of side BC is x−y=0. The circumcenter and orthocentre of triangle are (2, 3) and (5, 8), respectively. The equation of the circumcirle of the triangle is a) x2+y2−4x+6y−27=0 b) x2+y2−4x−6y−27=0 c) x2+y2+4x−6y−27=0 d) x2+y2+4x+6y−27=0
x2+y2−4x−6y−27=0
x2+y2−4x−6y−36=0
x2+y2−4x−6y−24=0
x^(2)+y^(2)-4x-6y-15=0
The correct Answer is:2
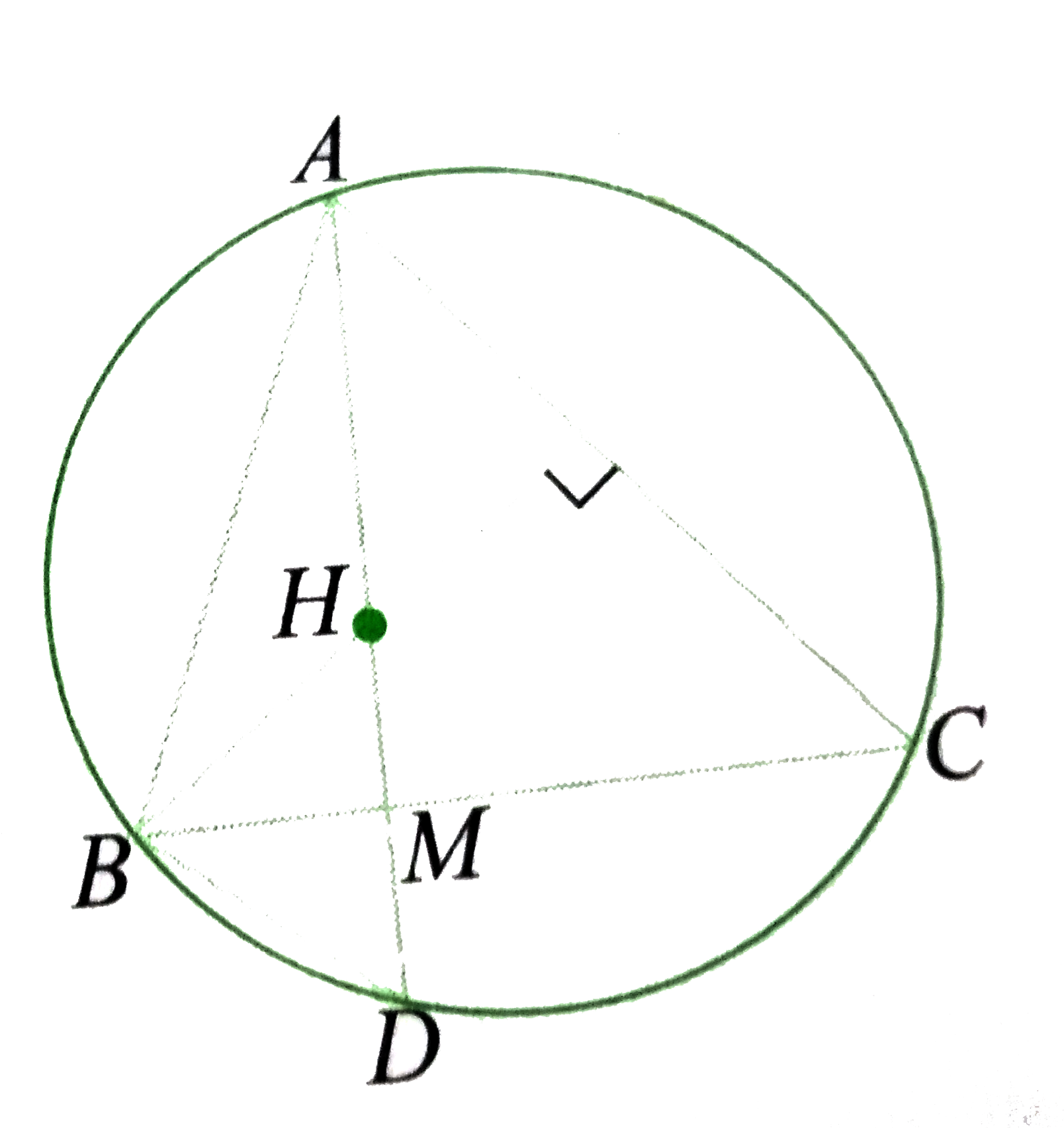
Let the orthocenter be H(5,8)
Now, ∠HBM=π2−C
Also, ∠DBC=∠DAC=π2−C
Hence, ΔCMH and ΔBMD are congruent. Therefore,
HM=MD
D is the image of H in the line x−y=0, which is D(8,5).
Thus, the equation of the circumcircle is
(x−2)2+(y−3)2=(8−2)2+(5−3)2
i.e., x2+y2−4x−6y−6y−27=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.20
1 Video
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Find the equation of the radical axis of the following circles.
x2+y2−2x−4y−1=0
x2+y2−4x−6y+5=0
View SolutionThe equation of the circle which cuts the three circles x2+y2−4x−6y+4=0,x2+y2−2x−8y+4=0,x2+y2−6x−6y+4=0 orthogonally is
View SolutionThe equation of the circle which cuts orthogonally the three circles x2+y2+4x+2y+1=0,2x2+2y2+8x+6y−3=0,x2+y2+6x−2y−3=0 is
View SolutionFind the radical centre of the following circles
x2+y2−4x−6y+5=0
x2+y2−2x−4y−1=0
x2+y2−6x−2y=0
View SolutionFind the equation of the circle which cuts the three circles x2+y2−3x−6y+14=0,x2+y2−x−4y+8=0, and x2+y2+2x−6y+9=0 orthogonally.
View SolutionFind the length of the common chord of the circles x2+y2+2x+6y=0 and x2+y2−4x−2y−6=0
View SolutionFind the equation of the circle which cuts the circles x2+y2+4x+2y+1=0,2(x2+y2)+8x+6y−3=0 and x2+y2+6x−2y−3=0 orthogonally.
View SolutionFind the equation of the common chord of the following pair of circles
x2+y2−4x−4y+3=0
x2+y2−5x−6y+4=0
View SolutionThe radical centre of the circles x2+y2=9,x2+y2−2x−2y−5=0,x2+y2+4x+6y−19=0 is
View Solution(6,0),(0,6),and(7,7) are the vertices of a ABC . The incircle of the triangle has equation. a x2+y2−9x−9y+36=0 b x2+y2+9x−9y+36=0 c x2+y2+9x+9y−36=0 d x2+y2+18x−18y+36=0
View Solution
