Let f(x)=x+2|x+1|+2|x−1|. If f(x)=k has exactly one real solution, then the value of k is
3
0
1
2
The correct Answer is:A
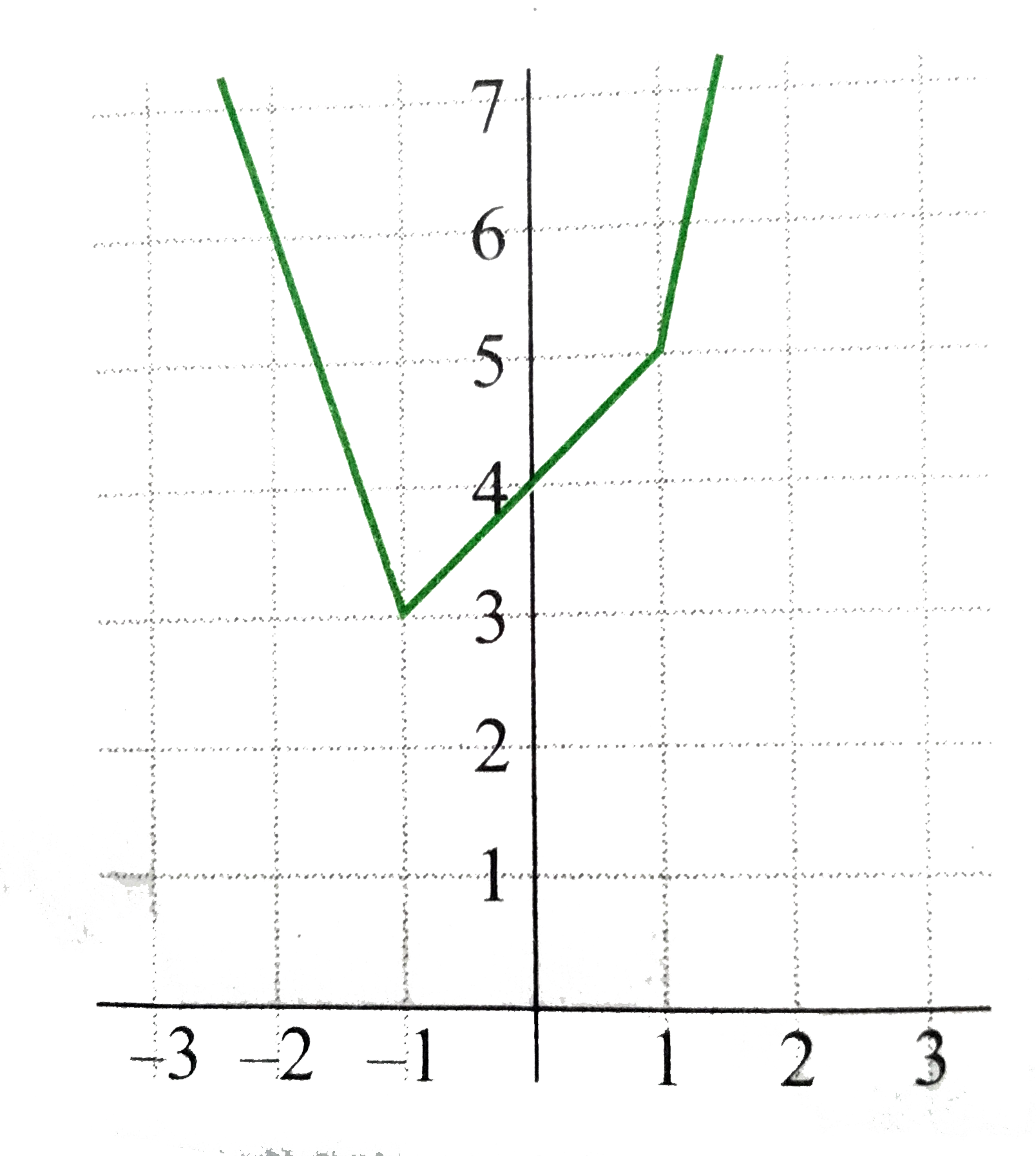
Let f(x)=x+2|x+1|+2|x−1|
=⎧⎪⎨⎪⎩x−2(x+1)−2(x−1),x<−1x+2(x+1)−2(x−1),−1≤x≤1x+2(x+1)+2(x−1),x>1
=⎧⎪⎨⎪⎩−3x,x<−1x+4,−1≤x≤15x,x>1
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Multiple Correct Answer Type
27 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Linked Comprehension Type
32 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.15
8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Let f(x)=x+2|x+1|+2|x−1|. If f(x)=k has exactly one real solution, then the value of k is (a)3 (b) 0 (c)1 (d) 2
View SolutionLet f(x)=x+2|x+1|+x−1∣.Iff(x)=k has exactly one real solution, then the value of k is 3 (b) 0 (c) 1 (d) 2
View SolutionLet f(x)=x+2|x+1|+2|x−1|. Find the values of k if f(x)=k
(i) has exactly one real solution,
(ii) has two negative solutions,
(iii) has two solutions of opposite sign.
View SolutionIf f(x)=x2 is a real function, find the value of f(1).
View SolutionLet f(x)=sin−1x+∣∣sin−1x∣∣+sin−1|x| If the equation f(x) = k has two solutions, then true set of values of k is
View SolutionIf the equation xlogax2=xk−2ak,a≠0has exactly one solution for x, then the value of k is/are
View SolutionConsider the polynomial f(x)=1+2x+3x2+4x3 for all x∈R So f(x) has exactly one real root in the interval
View SolutionLet f(x)=3x−2+4x−3+5x−4. Then f(x)=0 has (A) exactly one real root in (2,3) (B) exactly one real root in (3,4) (C) at least one real root in (2,3) (D) none of these
View SolutionLet f(x)=|x−1|+|x−2|+|x−3| , match the column I for the value of k column II.
Column - I Column -II(A) f(x) = k has no solution (p) 1 (B) f(x)=k has only one solution(q) 2 (C) f(x) = k has two solution of same sign (r) 4(D) f(x)= k has two solution of opposite sign(s) 5(t) 8
View SolutionLet f:R→R be defined by f(x)={k−2x,ifx≤−1(−2x+3),x≻1} . If f has a local minimum at x=−1 , then a possible value of k is (1) 0 (2) −12 (3) −1 (4) 1
View Solution
