Find f(x) when it is given by
f(x)=max{x3,x2,164},∀x∈[0,∞).
f(x)={x2,0≤x≤1x3,x>1
f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩164,0≤x≤14x2,14<x≤1x3,x>1
f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩164,0≤x≤18x2,18<x≤1x3,x>1
f(x)={164,0≤x≤18x3,x>1/8
The correct Answer is:C
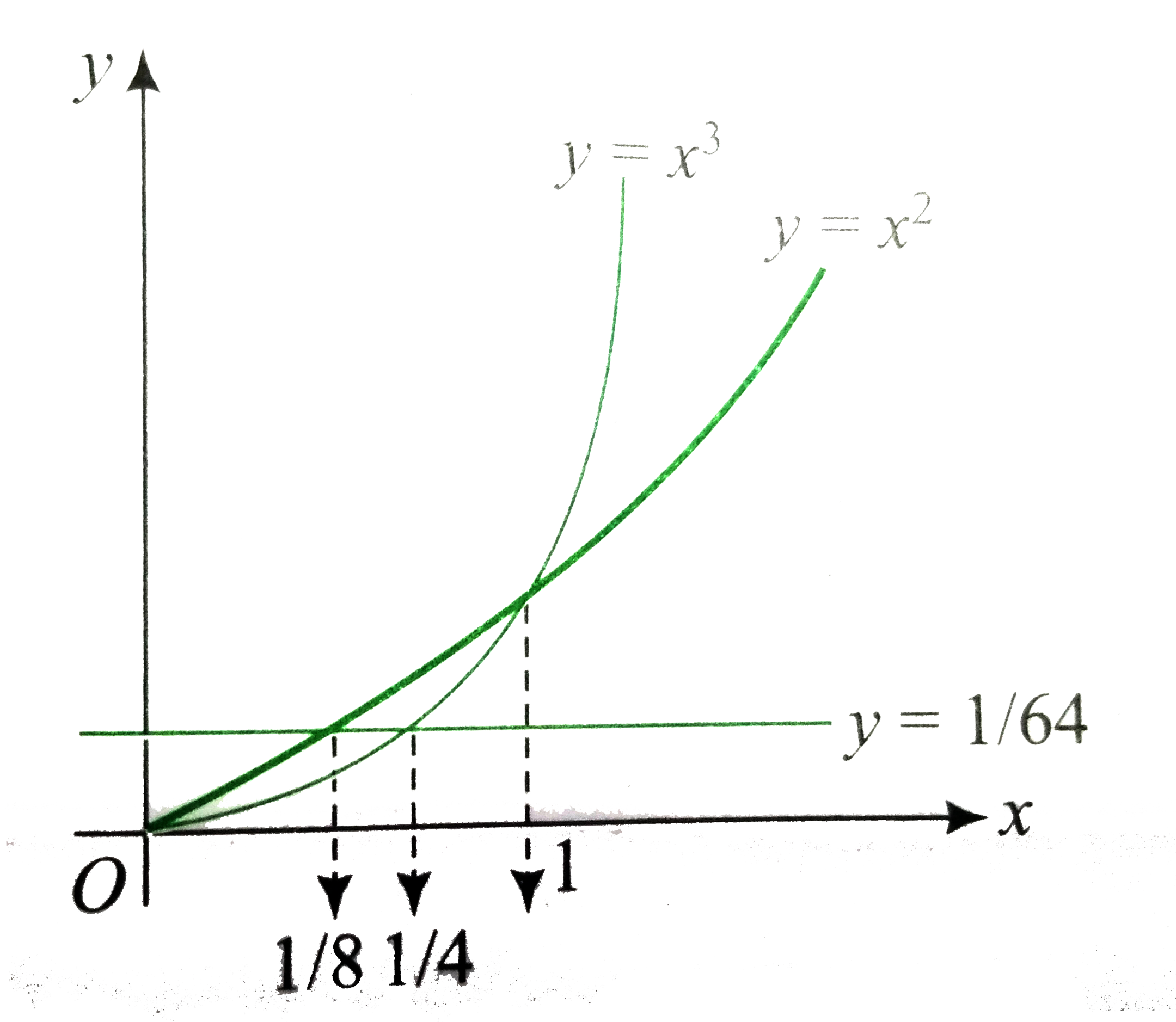
Clearly, from the graph, f(x)=⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩164,0≤x≤18x2,18<x≤1x3,x>1
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Multiple Correct Answer Type
27 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Linked Comprehension Type
32 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.15
8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
The function f(x)=max{(1−x),(1+x),2},x∈(−∞,∞) is
View SolutionLet fnx+fn(y)=xn+ynxnyn∀x,y∈R−{0}. where n∈N and g(x)=max{f2(x),f3(x),12}∀x∈R−{0}
The number of values of x for which g(x) is non-differentiable (x∈R−{0}):
View SolutionLet f[1,2]→(−∞,∞) be given by f(x)=x4+3x2+1x2+1 then find value of in [fmax] in [−1,2] where [.] is greatest integer function :
View SolutionIf f(x)=max.(x4,x2,181)∀x∈[0,∞), then the sum of square of reciprocal of all the values of x where f (x) is non-differentiable, is equal to:
View SolutionSuppose f'(x) exists for each x and h(x)=f(x)−(f(x))2+(f(x))3∀x∈R, then
View SolutionFind critical points of f(x) =max (sinx cosx) ∀,X∈(0,2π).
View SolutionIf f(x)=max{x3,x2,164}∀x∈[0,∞),then f(x)={x2,0≤x≤1x3,x>0 f(x)={164,0≤x<=14x2,14<x≤1x3,x>1 f(x)={164,0≤x≤18x2,18<x≤1x3,x>1 f(x)={164,0≤x≤18x3,x>18
View SolutionSometimes functions are defined like f(x)=max{sinx,cosx}, then f(x) is splitted like f(x)=⎧⎪⎨⎪⎩cosxx∈(0,π4]sinxx∈(π4,π2] etc.
If f(x)=max{12,sinx}, then f(x)=12 is defined when x∈
View SolutionSometimes functions are defined like f(x)=max{sinx,cosx}, then f(x) is splitted like f(x)=⎧⎪⎨⎪⎩cosxx∈(0,π4]sinxx∈(π4,π2] etc.
If f(x)=max{x2,2x},then if x∈(0,1), f(x)=
View SolutionFind the equivalent definition of f(x)=max{x2,(1−x)2,2x(1−x)}where 0≤x≤1
View Solution
