If f(2x+y8,2x−y8)=xy , then f(m,n)=0 only when m=n only when m≠n onlywhenm=−n (d) forallmandn
only when m=n
only when m≠n
only when m=−n
for all m and n
The correct Answer is:D
To solve the problem, we start with the given function:
f(2x+y8,2x−y8)=xy
We need to find the conditions under which f(m,n)=0.
Step 1: Define Variables
Let:
- α=2x+y8
- β=2x−y8
From the given equation, we know:
f(α,β)=xy
Step 2: Solve for x and y
We can derive x and y from α and β.
1. Adding the equations:
α+β=(2x+y8)+(2x−y8)=4x
Thus, we have:
x=α+β4
2. Subtracting the equations:
α−β=(2x+y8)−(2x−y8)=y4
Thus, we have:
y=4(α−β)
Step 3: Substitute Back into the Function
Now substituting x and y back into the function:
f(α,β)=(α+β4)⋅(4(α−β))
This simplifies to:
f(α,β)=(α+β)(α−β)=α2−β2
Step 4: Express f(m,n)
Now, if we let m=α and n=β, we have:
f(m,n)=m2−n2
Step 5: Analyze f(m,n)=0
Setting f(m,n)=0:
m2−n2=0
This implies:
m2=n2
Step 6: Solve for Conditions
The equation m2=n2 can be factored as:
(m−n)(m+n)=0
This gives us two cases:
1. m−n=0 → m=n
2. m+n=0 → m=−n
Conclusion
Thus, f(m,n)=0 under the conditions:
- m=n
- m=−n
However, since the problem asks for when f(m,n)=0, we conclude that it holds true for all values of m and n because both conditions can occur simultaneously.
Final Answer
The correct answer is:
(d) for all m and n.
Let:
- α=2x+y8
- β=2x−y8
We can derive x and y from α and β.
α+β=(2x+y8)+(2x−y8)=4x
Thus, we have:
x=α+β4
α−β=(2x+y8)−(2x−y8)=y4
Thus, we have:
y=4(α−β)
Now substituting x and y back into the function:
Now, if we let m=α and n=β, we have:
Setting f(m,n)=0:
The equation m2=n2 can be factored as:
2. m+n=0 → m=−n
Thus, f(m,n)=0 under the conditions:
- m=n
- m=−n
The correct answer is:
(d) for all m and n.
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:Multiple Correct Answer Type
Explore 27 Videos
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:Linked Comprehension Type
Explore 32 Videos
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:CONCEPT APPLICATION EXERCISE 1.15
Explore 8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Archives (Numerical Value Type)
Explore 3 Videos
- SCALER TRIPLE PRODUCTS Book:CENGAGE ENGLISHChapter:SCALER TRIPLE PRODUCTS Exercise:DPP 2.3
Explore 11 Videos
Similar Questions
If f(2x+y8,2x−y8)=xy , then f(m,n)+f(n,m)=0 (a) only when m=n (b) only when m≠n (c) only when m=−n (d) for all m and n
View SolutionIf x and y vary inversely, find the values of l, m and n :

View SolutionIf x and y vary inversely, find the values of l, m and n :
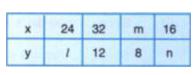
View SolutionLet m and n be positive integers and x,y>0andx+y=k, where k is constant. Let f(x,y)=xmyn, then: (a) f(x,y) is maximum when x=mkm+n (b) f(x,y) is maximuim where x=y (c) maximum value of f(x,y) is mnnmkm+n(m+n)m+n (d) maximum value of f(x,y) is km+nmmnn(m+n)m+n
View SolutionIf the segment intercepted by the parabola y2=4ax with the line lx+my+n=0 subtends a right angle at the vertex, then 4al+n=0 (b) 4al+4am+n=0 4am+n=0 (d) al+n=0
View SolutionIf nCx= nCy and x≠y, then x+y=n.
View SolutionIf the only point of inflection of the function f(x)−(x−a)m(x−b)n , m,neN and m≠n is at x=a then
View SolutionIf xmyn=(x+y)m+n , prove that d2ydx2=0 .
View SolutionIf f(x+y)=f(x)+f(y)−xy−1 for all x,y, and f(1)=1 then the number of solutions of f(n)=n,n∈N, is
(a) one
(b) two
(c) four
(d) none of these
View SolutionIf f(x+y)=f(x)+f(y)−xy−1∀x,y∈Randf(1)=1, then the number of solution of f(n)=n,n∈N, is 0 (b) 1 (c) 2 (d) more than 2
View Solution