Let P={(x,y)∣x2+y2=1,x,y∈R}. Then, R, is
Reflexive
Symmetric
Transitive
Anti-symmetric
The correct Answer is:B
To determine the properties of the relation R={(x,y)|x2+y2=1,x,y∈R}, we will check if it is reflexive, symmetric, transitive, or anti-symmetric.
Step 1: Check for Reflexivity
A relation R is reflexive if for every element x in the set, the pair (x,x) is in R.
- For (x,x) to be in R, we need:
x2+x2=1⟹2x2=1⟹x2=12⟹x=±1√2
- The pairs (1√2,1√2) and (−1√2,−1√2) are in R, but not all real numbers x have the pair (x,x) in R.
Conclusion: The relation R is not reflexive.
Step 2: Check for Symmetry
A relation R is symmetric if whenever (x,y) is in R, then (y,x) is also in R.
- Assume (x,y)∈R, meaning x2+y2=1.
- If we switch x and y, we have y2+x2=1, which is the same equation.
Conclusion: The relation R is symmetric.
Step 3: Check for Transitivity
A relation R is transitive if whenever (x,y) and (y,z) are in R, then (x,z) must also be in R.
- Assume (x,y)∈R and (y,z)∈R:
x2+y2=1andy2+z2=1
- From these, we cannot conclude that x2+z2=1. For example, let x=1,y=0,z=1:
- (1,0)∈R and (0,1)∈R, but (1,1)∉R since 12+12≠1.
Conclusion: The relation R is not transitive.
Step 4: Check for Anti-symmetry
A relation R is anti-symmetric if whenever (x,y)∈R and (y,x)∈R, then x=y.
- Since we found that R is symmetric, it cannot be anti-symmetric unless x=y for all pairs, which is not the case here.
Conclusion: The relation R is not anti-symmetric.
Final Conclusion
The relation R is symmetric but neither reflexive, transitive, nor anti-symmetric.
---
A relation R is reflexive if for every element x in the set, the pair (x,x) is in R.
x2+x2=1⟹2x2=1⟹x2=12⟹x=±1√2
- The pairs (1√2,1√2) and (−1√2,−1√2) are in R, but not all real numbers x have the pair (x,x) in R.
A relation R is symmetric if whenever (x,y) is in R, then (y,x) is also in R.
- If we switch x and y, we have y2+x2=1, which is the same equation.
A relation R is transitive if whenever (x,y) and (y,z) are in R, then (x,z) must also be in R.
x2+y2=1andy2+z2=1
- From these, we cannot conclude that x2+z2=1. For example, let x=1,y=0,z=1:
- (1,0)∈R and (0,1)∈R, but (1,1)∉R since 12+12≠1.
A relation R is anti-symmetric if whenever (x,y)∈R and (y,x)∈R, then x=y.
The relation R is symmetric but neither reflexive, transitive, nor anti-symmetric.
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Multiple Correct Answer Type
27 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Linked Comprehension Type
32 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.15
8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
ifA={(x,y):x2+y2≤1,x,y∈R]and
B={(x,y):x2+y2≤x2+y2≤4,x,y∈R]then
View SolutionifA={(x,y):x2+y2=4,x,y∈R}and
B={(x,y):Y=|x|,x,y∈R} then
View SolutionWhich of the following are function: {(x,y):y2=x,x,y∈R} b. {(x,y):y=|x|,x,y∈R} c. {(x,y):x2+y2=1,x,y∈R} d. {(x,y):x2−y2=1,x,y∈R}
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
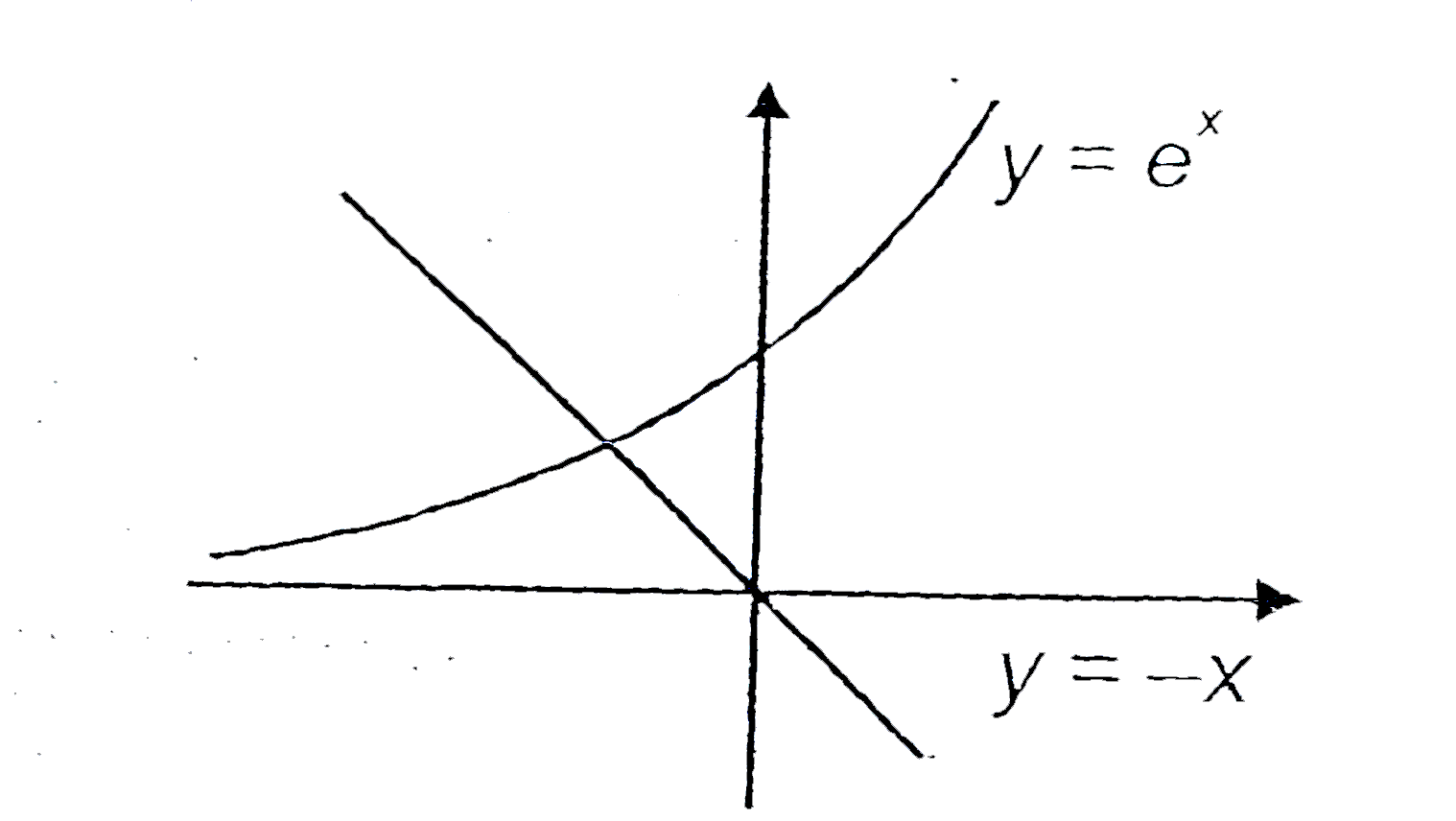
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
View SolutionLet f(x,y)=x2−y2andg(x,y)=2xy. such that (f(x,y))2−(g(x,y))2=12andf(x,y).G(x,y)=√34 Find the number of ordered pairs (x,y) ?
View SolutionLet A={1,2,3,...10} and R={(x,y):x+2y=10,x,y∈A} be a relation A. Then, R−1=
View SolutionLet x2+y2+xy+1≥a(x+y)∀x,y∈R, then the number of possible integer (s) in the range of a is___________.
View SolutionLet x2+y2+xy+1≥a(x+y)∀x,y∈R, then the number of possible integer (s) in the range of a is___________.
View SolutionLet f:R→R such that f(x+y)+f(x−y)=2f(x)f(y) for all x,y∈R. Then,
View SolutionLet f(x+y)−f(x)2=f(y)−12+xy, for all x,y∈R,f(x) is differentiable and f'(0)=1.
Range of y=log3/4(f(x)) is
View Solution
