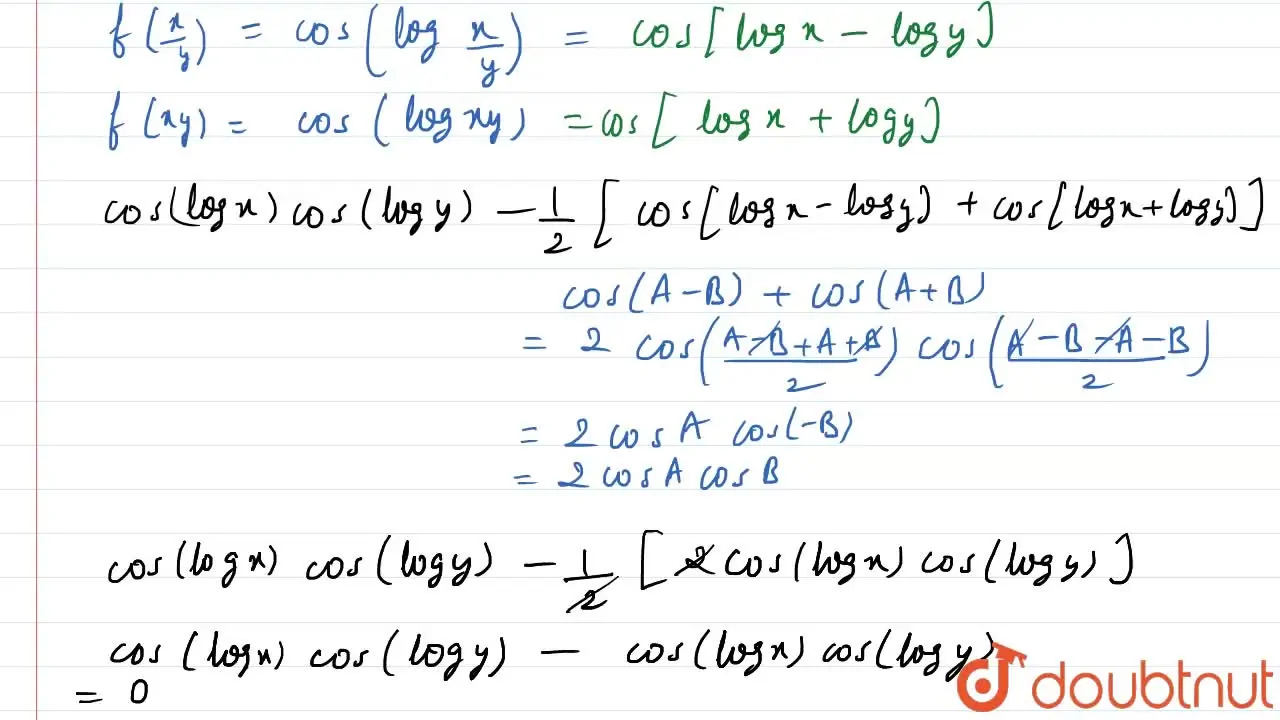If then has the value
-1
-2
0
The correct Answer is:D
or
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Multiple Correct Answer Type27videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Linked Comprehension Type32videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.158videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)3videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
If f(x)=cos((log)ex),thenf(x)f(y)−12[f(xy)+f(xy)] has value (a) −1 (b) 12 (c) −2 (d) none of these
View SolutionIf f(x)=cos((log)ex),thenf(x)f(y)−12[f(xy)+f(xy)] has value (a) −1 (b) 12 (c) −2 (d) none of these
View SolutionIf f(x)=cos((log)ex), then f(1x)f(1y)−12{f(xy)+f(xy)} is equal to a.cos(x−y) b. log(cos(x−y)) c. 0 d. cos(x+y)
View SolutionIf f(x)=cos(logx), then f(x2)f(y2)−12[f(x2y2)+f(x2y2)]=
View SolutionIf f(x)=sin(logx) then f(xy)+f(xy)−2f(x)cos(logy)= (A) cos(logx) (B) sin(logy) (C) cos(log(xy)) (D) 0
View SolutionIf f(x+y,x−y)=xy then f(x,y)+f(y,x)2=
View SolutionIf f(x)=cos(logx), then prove that
f(1x).f(1y)−12[f(xy)+f(xy)]=0View SolutionIf f(x)=logex, then prove that :f(xyz)=f(x)+f(y)+f(z)
View SolutionIf f'(x)=sin(logx)andy=f(2x+33−2x), then dydx equals
View SolutionLet f(x) is a polynomial satisfying f(x).f(y)=f(x)+f(y)+f(xy)−2 for all x,y and f(2)=1025, then the value of limx→2f'(x) is
View Solution