Given the function f(x)=ax+a−x2(wherea>2).Thenf(x+y)+f(x−y)= 2f(x).f(y) (b) f(x).f(y) f(x)f(y) (d) none of these
The correct Answer is:A
To solve the problem, we need to evaluate the expression f(x+y)+f(x−y) given the function f(x)=ax+a−x2 where a>2.
1. Define the function:
f(x)=ax+a−x2
2. Calculate f(x+y):
f(x+y)=ax+y+a−(x+y)2
3. Calculate f(x−y):
f(x−y)=ax−y+a−(x−y)2
4. Add f(x+y) and f(x−y):
f(x+y)+f(x−y)=ax+y+a−(x+y)2+ax−y+a−(x−y)2
Combine the fractions:
=ax+y+a−(x+y)+ax−y+a−(x−y)2
5. Factor out common terms:
Notice that ax+y and ax−y can be rewritten:
=12(axay+a−xa−y+axa−y+a−xay)
Rearranging gives:
=12(ax(ay+a−y)+a−x(ay+a−y))
6. Recognize the expression:
We can factor out ay+a−y:
=12(ay+a−y)(ax+a−x)
Since f(x)=ax+a−x2 and f(y)=ay+a−y2, we can rewrite:
=2f(x)f(y)
7. Final result:
Therefore, we have:
f(x+y)+f(x−y)=2f(x)f(y)
Conclusion:
The correct answer is 2f(x)⋅f(y).
f(x)=ax+a−x2
f(x+y)=ax+y+a−(x+y)2
f(x−y)=ax−y+a−(x−y)2
f(x+y)+f(x−y)=ax+y+a−(x+y)2+ax−y+a−(x−y)2
Combine the fractions:
=ax+y+a−(x+y)+ax−y+a−(x−y)2
Notice that ax+y and ax−y can be rewritten:
=12(axay+a−xa−y+axa−y+a−xay)
Rearranging gives:
=12(ax(ay+a−y)+a−x(ay+a−y))
We can factor out ay+a−y:
=12(ay+a−y)(ax+a−x)
Since f(x)=ax+a−x2 and f(y)=ay+a−y2, we can rewrite:
=2f(x)f(y)
Therefore, we have:
f(x+y)+f(x−y)=2f(x)f(y)
The correct answer is 2f(x)⋅f(y).
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Multiple Correct Answer Type
27 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Linked Comprehension Type
32 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.15
8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Given the function f(x)=ax+a−x2(wherea>2).Thenf(x+y)+f(x−y)= (A) 2f(x).f(y) (B) f(x).f(y) (C) f(x)f(y) (D) none of these
View SolutionLet f(x)=|x−1|. Then (a)f(x2)=(f(x))2 (b) f(x+y)=f(x)+f(y) (c)f(|x|)=|f(x)| (d) none of these
View SolutionLet f(x)=|x−1|. Then (a)f(x2)=(f(x))2 (b) f(x+y)=f(x)+f(y) (c)f(|x|)=|f(x)| (d) none of these
View SolutionIf f(x)=limn→∞n(x1n−1),thenforx>0,y>0,f(xy) is equal to : (a)f(x)f(y) (b) f(x)+f(y) (c)f(x)−f(y) (d) none of these
View SolutionLet f(x+y)+f(x−y)=2f(x)f(y)∀x,y∈R and f(0)=k, then
View SolutionIf f(x)=cos((log)ex),thenf(x)f(y)−12[f(xy)+f(xy)] has value (a) −1 (b) 12 (c) −2 (d) none of these
View SolutionIf f(x)=cos((log)ex),thenf(x)f(y)−12[f(xy)+f(xy)] has value (a) −1 (b) 12 (c) −2 (d) none of these
View SolutionA function f:R→R satisfies the equation f(x)f(y)−f(xy)=x+y∀x,y∈Randf(1)>0 , then
a. f(x)f−1(x)=x2−4 b. f(x)f−1(x)=x2−6
c. f(x)f−1(x)=x2−1 d. none of these
View SolutionWhich of the following functions have the graph symmetrical about the origin? (a) f(x) given by f(x)+f(y)=f(x+y1−xy) (b) f(x) given by f(x)+f(y)=f(x√1−y2+y√1−x2) (c) f(x) given by f(x+y)=f(x)+f(y)∀x,y∈R (d) none of these
View SolutionGiven the graph of y=f(x).
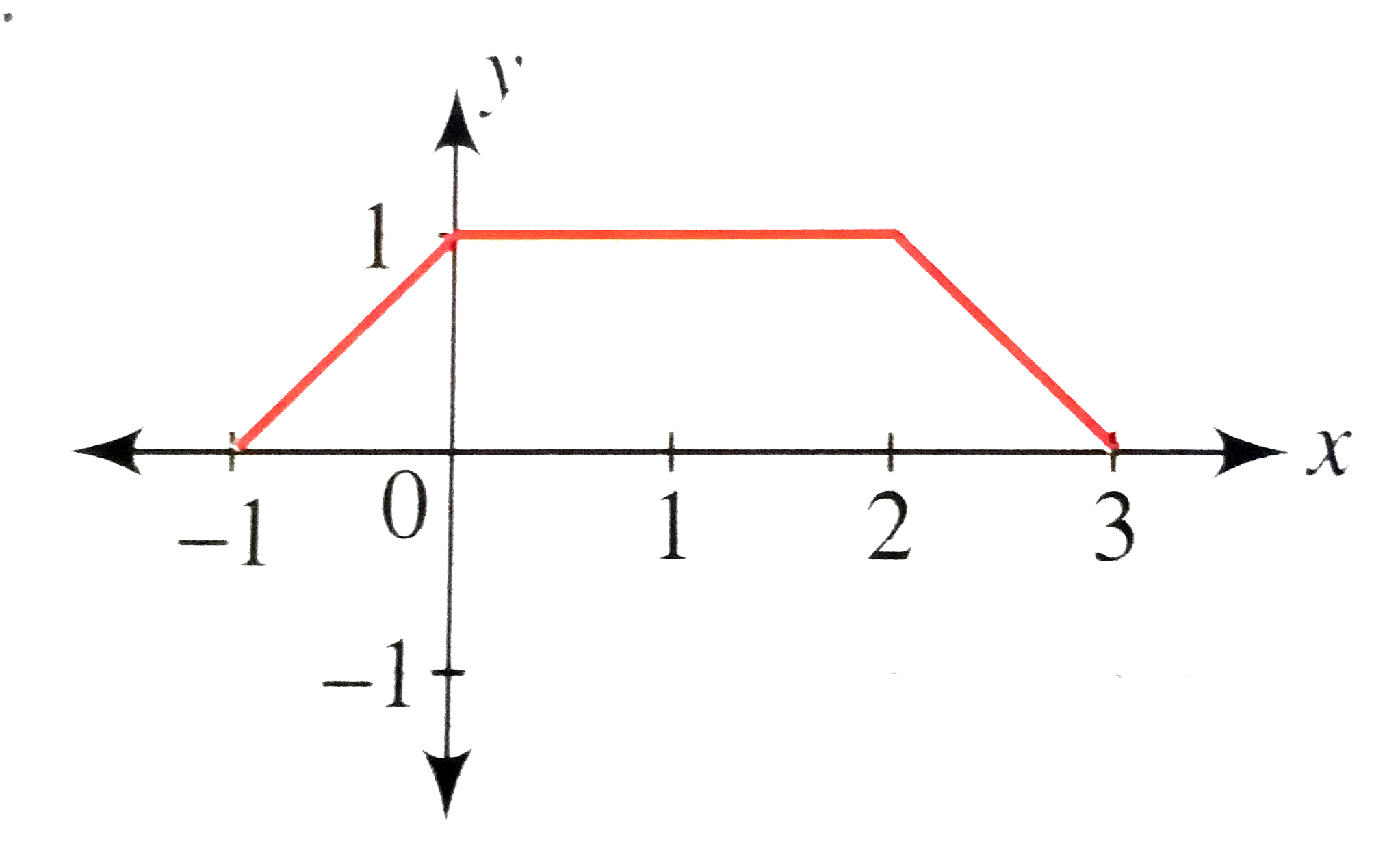
Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)
View Solution
