In an equilateral triangle, the inradius, circumradius, and one of the exradii are in the ratio
2:4:5
1:2:3
1:2:4
2:4:3
The correct Answer is:B
To solve the problem of finding the ratio of the inradius, circumradius, and one of the exradii of an equilateral triangle, we can follow these steps:
Step 1: Define the properties of the equilateral triangle
Let the side length of the equilateral triangle be a. In an equilateral triangle, all sides are equal, and we can denote the sides as a=b=c.
Step 2: Calculate the area of the triangle
The area Δ of an equilateral triangle is given by the formula:
Δ=√34a2
Step 3: Calculate the semi-perimeter S
The semi-perimeter S of the triangle is given by:
S=a+b+c2=3a2
Step 4: Calculate the inradius r
The inradius r can be calculated using the formula:
r=ΔS
Substituting the values from Steps 2 and 3:
r=√34a23a2=√3a24⋅23a=a2√3
Step 5: Calculate the circumradius R
The circumradius R can be calculated using the formula:
R=abc4Δ
For an equilateral triangle, this simplifies to:
R=a⋅a⋅a4⋅√34a2=a3√3a2=a√3
Step 6: Calculate one of the exradii r1
The exradius r1 can be calculated using the formula:
r1=ΔS−a
Substituting the values:
r1=√34a23a2−a=√34a2a2=√32a
Step 7: Find the ratio of r:R:r1
Now we have:
- r=a2√3
- R=a√3
- r1=√32a
To find the ratio, we can express them in terms of a:
r:R:r1=a2√3:a√3:√32a
Dividing each term by a:
12√3:1√3:√32
Step 8: Simplify the ratio
To simplify:
1. Multiply each term by 2√3:
1:2:3
Thus, the ratio of the inradius, circumradius, and one of the exradii in an equilateral triangle is:
1:2:3
Final Answer
The correct option is 1:2:3.
Let the side length of the equilateral triangle be a. In an equilateral triangle, all sides are equal, and we can denote the sides as a=b=c.
The area Δ of an equilateral triangle is given by the formula:
Δ=√34a2
The semi-perimeter S of the triangle is given by:
S=a+b+c2=3a2
The inradius r can be calculated using the formula:
r=ΔS
Substituting the values from Steps 2 and 3:
r=√34a23a2=√3a24⋅23a=a2√3
The circumradius R can be calculated using the formula:
R=abc4Δ
For an equilateral triangle, this simplifies to:
R=a⋅a⋅a4⋅√34a2=a3√3a2=a√3
The exradius r1 can be calculated using the formula:
r1=ΔS−a
Substituting the values:
r1=√34a23a2−a=√34a2a2=√32a
Now we have:
- r=a2√3
- R=a√3
- r1=√32a
r:R:r1=a2√3:a√3:√32a
Dividing each term by a:
12√3:1√3:√32
To simplify:
1. Multiply each term by 2√3:
1:2:3
1:2:3
The correct option is 1:2:3.
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Multiple correct answer type
24 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Linked comprehension type
34 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.11
4 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
Knowledge Check
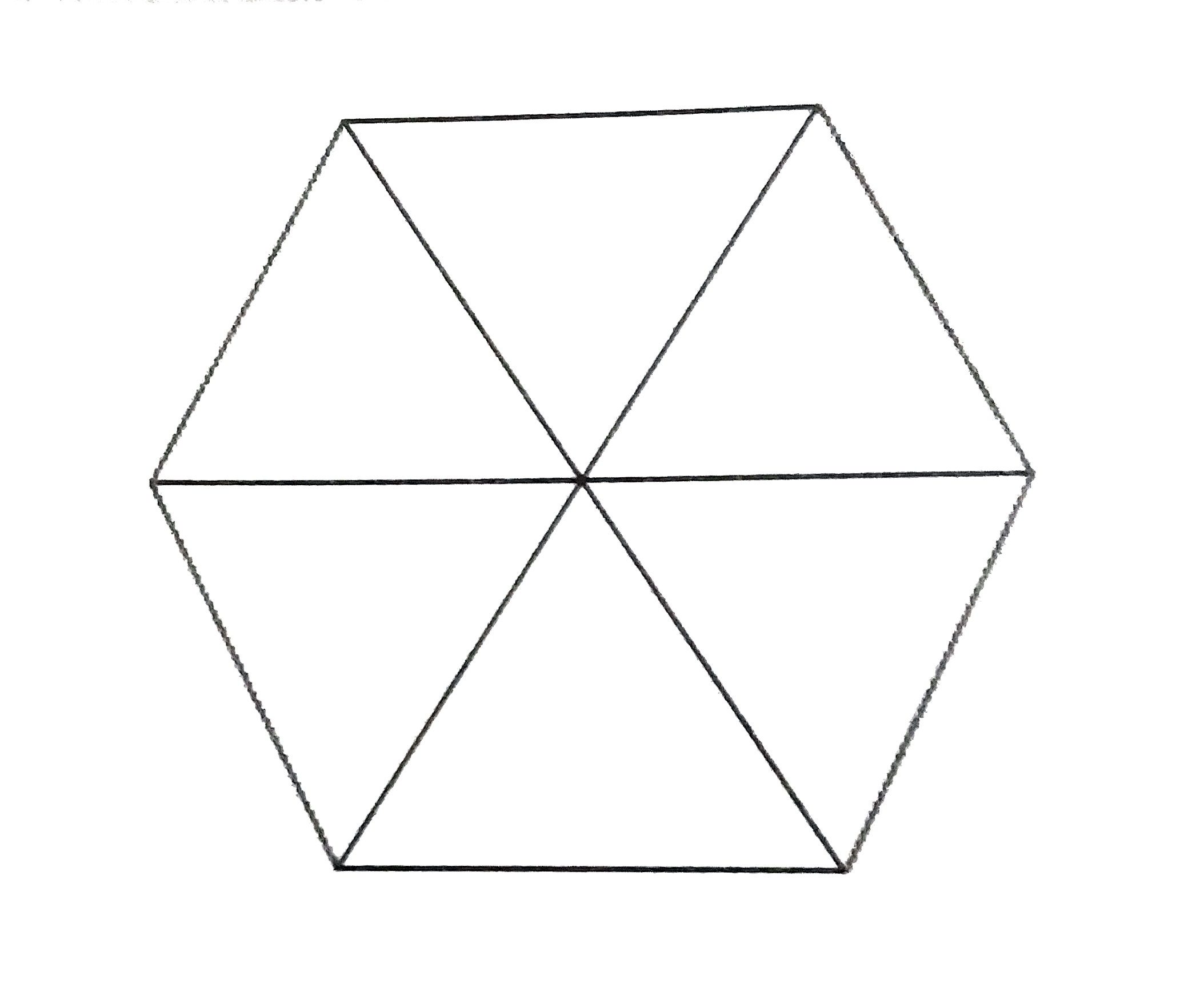
The regular hexagon shown above is divided into six congruent equilateral triangle. What is the measure, in degrees, of one of the interior angles of the hexagon?A60∘B120∘C180∘D360∘
In an equilateral triangle, if inradius is a rational number then
View SolutionIn an equilateral triangle, the inradius and the circumradius are connected by r=4R b. r=R/2 c. r=R/3 d. none of these
View SolutionThe sides of a triangle are in A.P. and its area is 35th of the an equilateral triangle of the same perimeter, prove that its sides are in the ratio 3:5:7, and find the greatest angle of the triangle.
View SolutionIn a right-angled isosceles triangle, the ratio of the circumradius and inradius is
View SolutionIf the points z1,z2,z3 are the vertices of an equilateral triangle in the Argand plane, then which one of the following is not correct?
View SolutionLet A (3,2) and B (5,1). ABP is an equilateral triangle is constructed one the side of AB remote from the origin then the orthocentre of triangle ABP is:
View SolutionIn a right - angled isosceles triangle , the ratio of the circumradius and inradius is
View Solution
