In a cyclic quadrilateral PQRS, PQ= 2 units, QR= 5 units, RS=3 units and ∠PQR=600, then what is the measure of SP?
To find the measure of side SP in the cyclic quadrilateral PQRS, we can follow these steps:
Step 1: Understand the Given Information
We are given:
- PQ = 2 units
- QR = 5 units
- RS = 3 units
- Angle PQR = 60 degrees
Step 2: Use the Cosine Rule in Triangle PQR
In triangle PQR, we can apply the cosine rule to find the length of PR. The cosine rule states:
PR2=PQ2+QR2−2⋅PQ⋅QR⋅cos(∠PQR)
Substituting the known values:
PR2=22+52−2⋅2⋅5⋅cos(60∘)
Step 3: Calculate PR^2
Calculating the squares and cosine:
PR2=4+25−2⋅2⋅5⋅12
PR2=4+25−10
PR2=29−10=19
Thus, we have:
PR=√19
Step 4: Use the Cosine Rule in Triangle PSR
Now, we will apply the cosine rule in triangle PSR to find SP. Let SP = x. According to the cosine rule:
PR2=PS2+SR2−2⋅PS⋅SR⋅cos(∠PSR)
Here, we know:
- PR = √19
- PS = x
- SR = 3
- Angle PSR = 120 degrees (since opposite angles in a cyclic quadrilateral are supplementary)
Substituting these values into the cosine rule:
19=x2+32−2⋅x⋅3⋅cos(120∘)
Step 5: Calculate the Cosine of 120 Degrees
Since cos(120∘)=−12, we substitute this value:
19=x2+9+3x
Step 6: Rearrange the Equation
Rearranging gives:
x2+3x+9−19=0
x2+3x−10=0
Step 7: Solve the Quadratic Equation
Now we can solve the quadratic equation x2+3x−10=0 using the factorization method:
(x−2)(x+5)=0
This gives us two solutions:
1. x−2=0 → x=2
2. x+5=0 → x=−5 (not valid as length cannot be negative)
Thus, the valid solution is:
SP=2 units
Final Answer
The measure of SP is 2 units.
---
We are given:
- PQ = 2 units
- QR = 5 units
- RS = 3 units
- Angle PQR = 60 degrees
In triangle PQR, we can apply the cosine rule to find the length of PR. The cosine rule states:
PR2=PQ2+QR2−2⋅PQ⋅QR⋅cos(∠PQR)
PR2=22+52−2⋅2⋅5⋅cos(60∘)
Calculating the squares and cosine:
PR2=4+25−2⋅2⋅5⋅12
PR2=4+25−10
PR2=29−10=19
PR=√19
Now, we will apply the cosine rule in triangle PSR to find SP. Let SP = x. According to the cosine rule:
PR2=PS2+SR2−2⋅PS⋅SR⋅cos(∠PSR)
- PR = √19
- PS = x
- SR = 3
- Angle PSR = 120 degrees (since opposite angles in a cyclic quadrilateral are supplementary)
19=x2+32−2⋅x⋅3⋅cos(120∘)
Since cos(120∘)=−12, we substitute this value:
19=x2+9+3x
Rearranging gives:
x2+3x+9−19=0
x2+3x−10=0
Now we can solve the quadratic equation x2+3x−10=0 using the factorization method:
(x−2)(x+5)=0
1. x−2=0 → x=2
2. x+5=0 → x=−5 (not valid as length cannot be negative)
SP=2 units
The measure of SP is 2 units.
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.1
12 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.2
8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
In a cyclic -quadrilateral PQRS angle PQR =135∘ , Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A:∠B=2:1. find angles A and B
View SolutionPQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR=670 and ∠SPR=720, then ∠QRS= (a) 410 (b) 230 (c) 670 (d) 180
View Solution
Knowledge Check
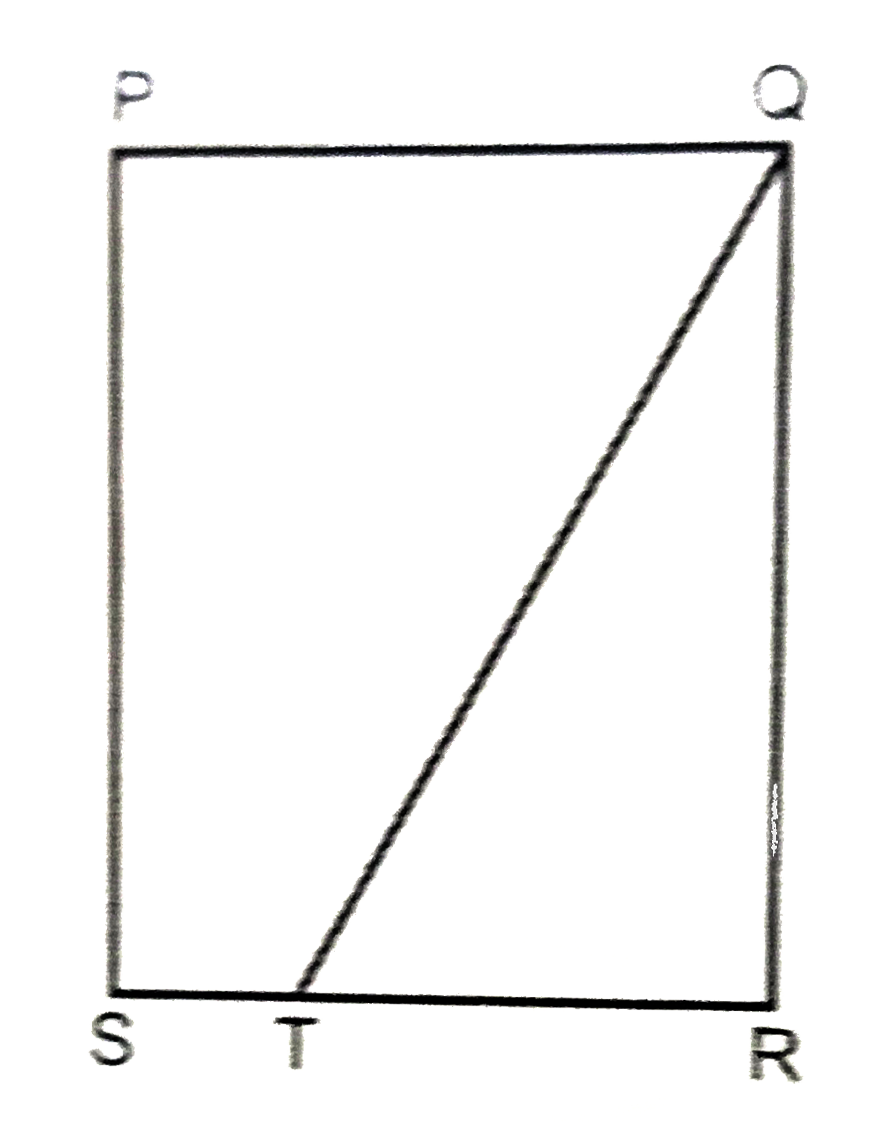
PQRS is a rectangle. T is a point on RS such that ST=2. If the area of the triangle QRT is 24 and QR : RS=2 : 1, what is the measure of QR?A12B14C15D16If map distance between genes P and Q is 4 units, between P and R is 11 units, and between Q and R is 7 units, the order of genes on the linkage map can be traced as follows
A B
B C
C D
D
Construct a quadrilateral PQRS, in which ∠Q=450,∠R=900,QR=5cm,PQ=9cmandRS=7cm
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View SolutionIn the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T. If SP=12cm and QR=4cm,
(iii) Find area of quadrilateral PQRS if area of ΔPTS=27cm2.

View SolutionTwo vectors 3 units and 5 units are acting at 60∘ to each other .What is the magnitude and direction of the resultant ?
View SolutionABCDEF is a regular hexagon , with the sides AB, AC, AD, AE and AF representing vectors 1 unit , 2 units , 3 units , 4 units and 5 units respetively . Find their resultant ?
View SolutionIn △ABC,P,Q,R are the feet of angle bisectors from the vertices to their opposite sides as shown in the figure. △PQR is constructed
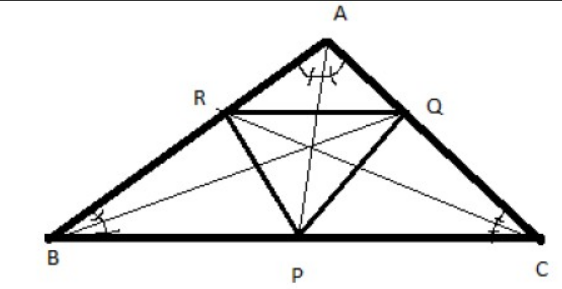
If AB=7 units, BC = 8 units, AC = 5 units, then the side PQ will be
View Solution
