Each side of triangle ABC is divided into three equal parts. Find the ratio of the area of hexagon PQRSTU to the area of the triangle ABC.
Area of hexagon PQRSTU
Δ1= area of ΔABC− area of ΔAPQ− area of ΔBTU− area of ΔCRS
=Δ−12(b3.c3sinA)−12(a3.c3sinB)−12(a3.b3sinC)
=Δ−Δ3=2Δ3
∴Δ1Δ=23
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.1
12 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.2
8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
ABCD is a parallelogram. Find the ratio of the area of Δ ABC to the area of the parallelogram ABCD.
View SolutionP is a point inside the triangle ABC. Lines are drawn through P, parallel to the sides of the triangle.The three resulting triangles with the vertex at P have areas 4,9and49sq. units. The area of the triangle ABC is -
View Solution
Knowledge Check
In the figure, what is the area of ΔABC?
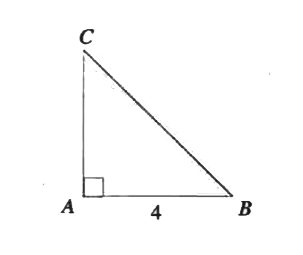 A6B7C8DIt cannot be determined from the information given
A6B7C8DIt cannot be determined from the information givenIn the figure, what is the area of ΔABC?
 A2B√2C1D1/2
A2B√2C1D1/2If the area of △ABC is 21, and the length of the height minus the length of the base equals 1, which of the following is equal to the base of the triangle ?
A2B4C6D7
Sides of triangle ABC, a, b, c are in G.P. If 'r' be the common ratio of this G.P. , then
View SolutionIn the given figure, ABC is a right angled triangle with ∠BAC=90∘.

Find the ratio of the area of DetlaADB is to area of ΔCDA.
View SolutionIn a triangle ABC, prove that the ratio of the area of the incircle to that of the triangle is π:cot(A2)cot(B2)cot(C2)
View SolutionIn the following figure ABC is a right angled triangle with ∠BAC=90∘,andAD⊥BC.
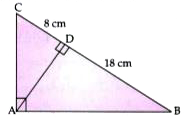
Find the ratio of the area of ΔADB to area of ΔCDA.
View SolutionAn equilateral triangle and a regular hexagon has same perimeter. Find the ratio of their areas.
View Solution
