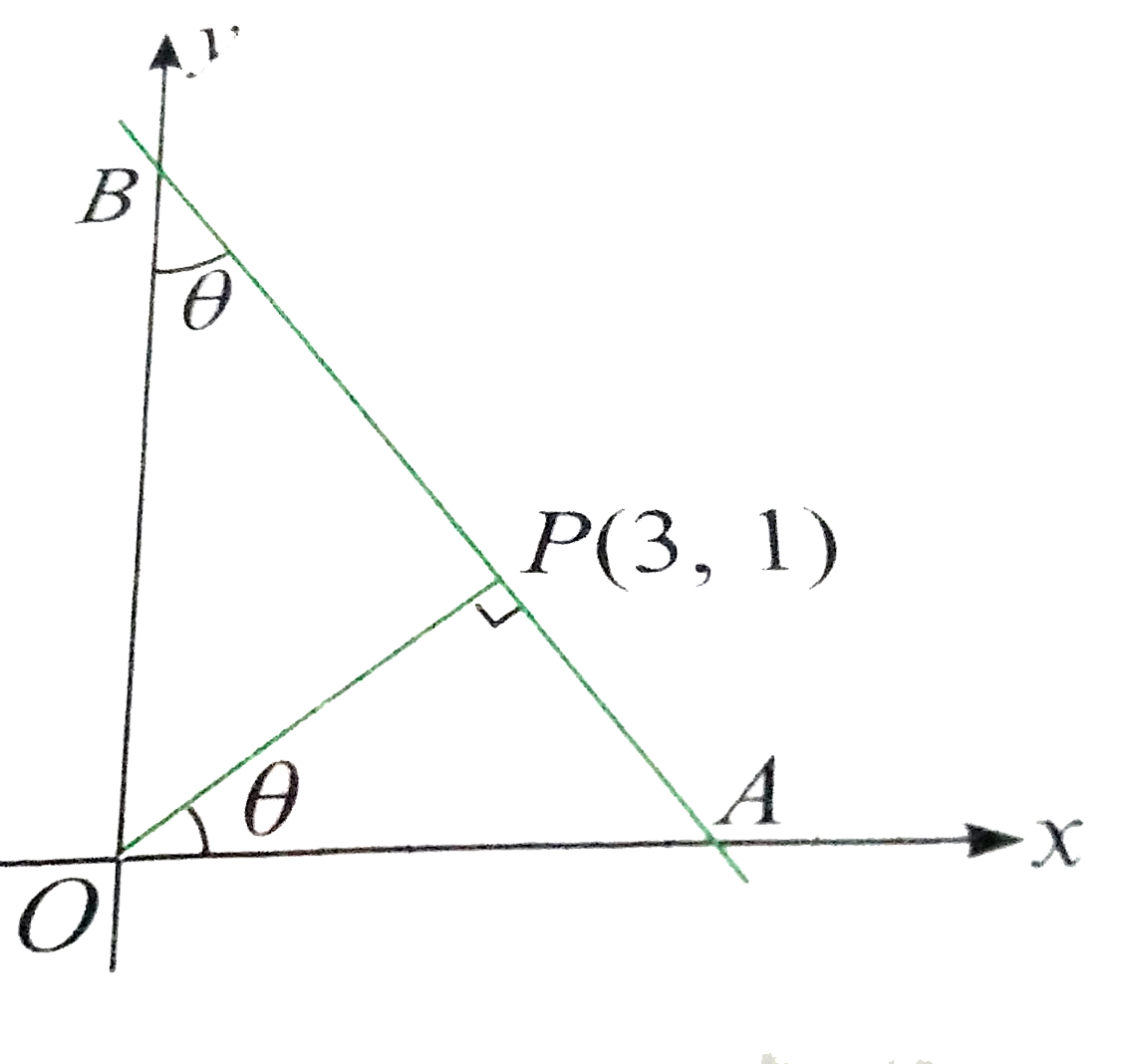
A straight line passing through P(3,1) meets the coordinate axes at AandB . It is given that the distance of this straight line from the origin O is maximum. The area of triangle OAB is equal to
50/3 sq.units
25/3 sq.units
20/3 sq.units
100/3 sq.units
The correct Answer is:A
Line AB will be the farthest from the origin if OP is right angled to the line drawn.
OP=√10
Also, tanθ=13
OA=OPsecθ
=√10×√103=10
OB=OPcosecθ=√10×√101=10
∴ Area of ΔOAB=12=12(103(10)=503
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct
13 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Linked
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.6
9 Videos
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
A variable line passing through point P(2,1) meets the axes at A and B . Find the locus of the circumcenter of triangle OAB (where O is the origin).
View SolutionA line is drawn through the point (1, 2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ, where O is the origin. If the area of the triangle OPQ is least, then the slope of the line PQ is
View SolutionA straight line l with negative slope passes through (8,2) and cuts the coordinate axes at P and Q. Find absolute minimum value of ''OP+OQ where O is the origin-
View SolutionA variable line through the point P(2,1) meets the axes at A an d B . Find the locus of the centroid of triangle OAB (where O is the origin).
View SolutionThe straight line xa+yb=1 cuts the coordinate axes at A and B . Find the equation of the circle passing through O(0,0),AandB.
View SolutionThe straight line through a fixed point (2,3) intersects the coordinate axes at distinct point P and Q. If O is the origin and the rectangle OPRQ is completed then the locus of R is
View SolutionA circle passes through the point (3,4) and cuts the circle x2+y2=c2 orthogonally, the locus of its centre is a straight line. If the distance of this straight line from the origin is 25. then a2=
View SolutionA straight line is drawn through P(3,4) to meet the axis of x and y at AandB , respectively. If the rectangle OACB is completed, then find the locus of C.
View SolutionA straight line passing through the point(2,2) and the axes enclose an area λ. The intercepts on the axes made by the line are given by the two roots of:
View SolutionA straight line passes through (2, 3) and the portion of the line intercepted between the axes is bisected at this point. Find its equation.
View Solution
