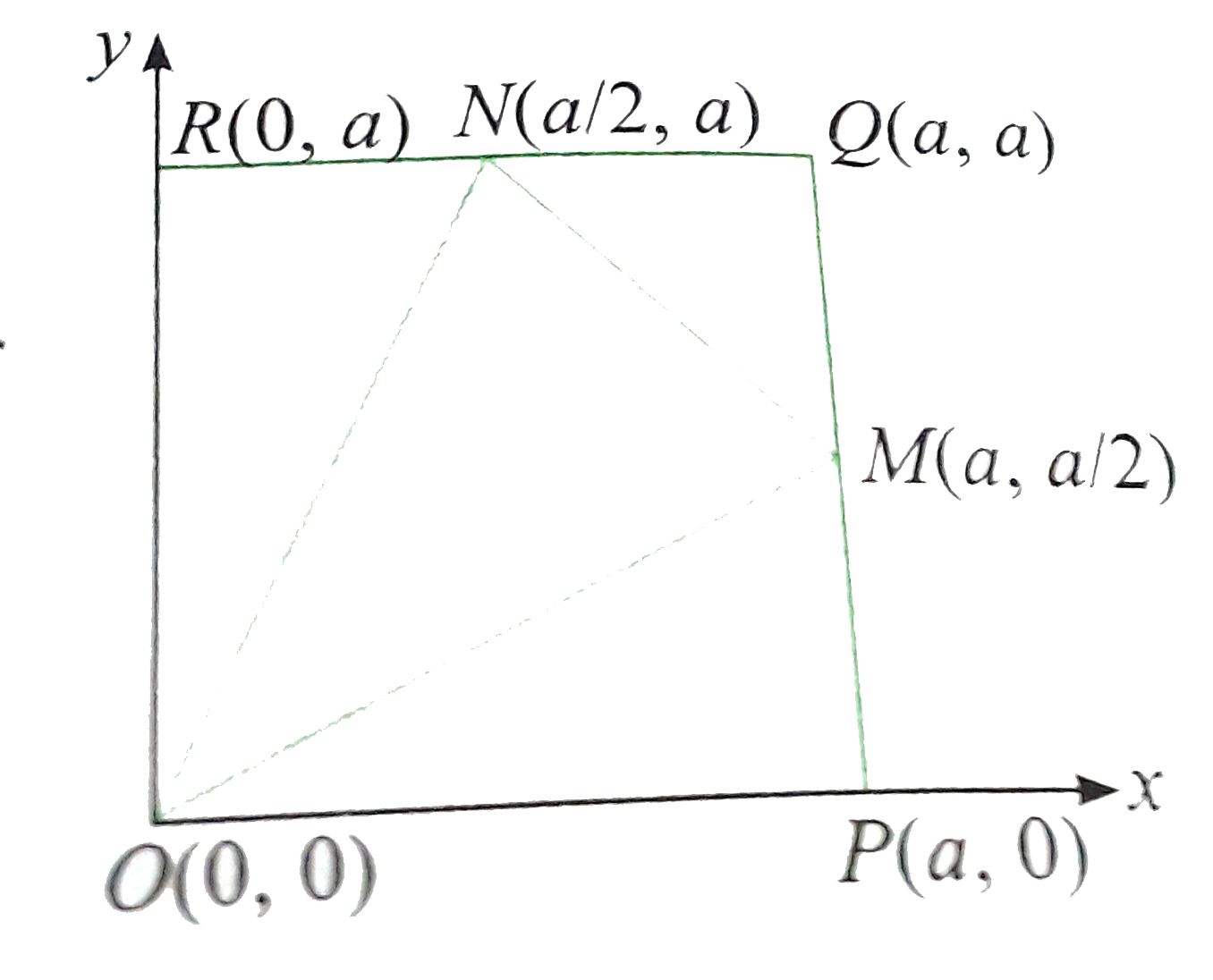
is a square and are the middle points of the sides , respectively. Then the ratio of the area of the square to that of triangle is 4:1 (b) 2:1 (c) 8:3 (d) 7:3
The correct Answer is:C
Let the coordinates of vertices be , resepectively. Then we get the coordiantes of M as and those of N as . Therefore, the area of is
The area of the sqaure is . Hence, the required ratio is .
Topper's Solved these Questions
- COORDINATE SYSYEM Book:CENGAGE ENGLISHChapter:COORDINATE SYSYEM Exercise:Multiple correct
Explore 13 Videos
- COORDINATE SYSYEM Book:CENGAGE ENGLISHChapter:COORDINATE SYSYEM Exercise:Linked
Explore 10 Videos
- COORDINATE SYSYEM Book:CENGAGE ENGLISHChapter:COORDINATE SYSYEM Exercise:Concept applications 1.6
Explore 9 Videos
- COORDINATE SYSTEMBook:CENGAGE ENGLISHChapter:COORDINATE SYSTEMExercise:Multiple Correct Answers Type
Explore 2 Videos
- CROSS PRODUCTS Book:CENGAGE ENGLISHChapter:CROSS PRODUCTS Exercise:DPP 2.2
Explore 13 Videos
Similar Questions
OPQR is a square and M,N are the middle points of the sides PQandQR , respectively. Then the ratio of the area of the square to that of triangle OMN is (a) 8:1 (b) 2:1 (c) 8:3 (d) 7:3
View SolutionOPQR is a square and M,N are the midpoints of the sides PQ and QR , respectively. If the ratio of the area of the square to that of triangle OMN is λ:6, then λ4 is equal to 2 (b) 4 (c) 2 (d) 16
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View SolutionIn A PQR, if PQ=QR and L, M and N are the mid-points of the sides PQ, PR and RP respectively. Prove that LN=MN
View SolutionIn triangle PQR, if PQ=RQ and L, M and N are the mid-points of the sides PQ, QR and RP respectively. Prove that LN=MN.
View SolutionThe ratio of the area of a square of side a and that of an equilateral triangle of side a, is (a) 2:1 (b) 2:√3 (c) 4:3 (d) 4:√3
View SolutionIn Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of △OTS if PQ=8 cm.
View SolutionThe line x+y=p meets the x- and y-axes at AandB , respectively. A triangle APQ is inscribed in triangle OAB,O being the origin, with right angle at Q.P and Q lie, respectively, on OBandAB . If the area of triangle APQ is 38th of the are of triangle OAB, the AQBQ is equal to (a)2(b) 23 (c) 13 (d)3
View SolutionIn two similar triangles ABC and PQR , if their corresponding altitudes AD and PS are in the ratio 4:9, find the ratio of the areas of triangle ABC and triangle PQR .
View SolutionIn square ABCD, P and Q are mid-point of AB and CD respectively. If AB=8cm and PQ and BD intersect at O, then find area of OPB
View Solution