Consider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one negative solution for a∈
(a) (−∞,2)
(b) (3,∞)
(c) (−2,∞)
(d) (2,3)
9x−a.3x−a+3≤0
Let t=3x
⇒ t2−at−a+3≤0
or t2+3≤a(t+1) (i)
where t∈R+ for ∀x∈R
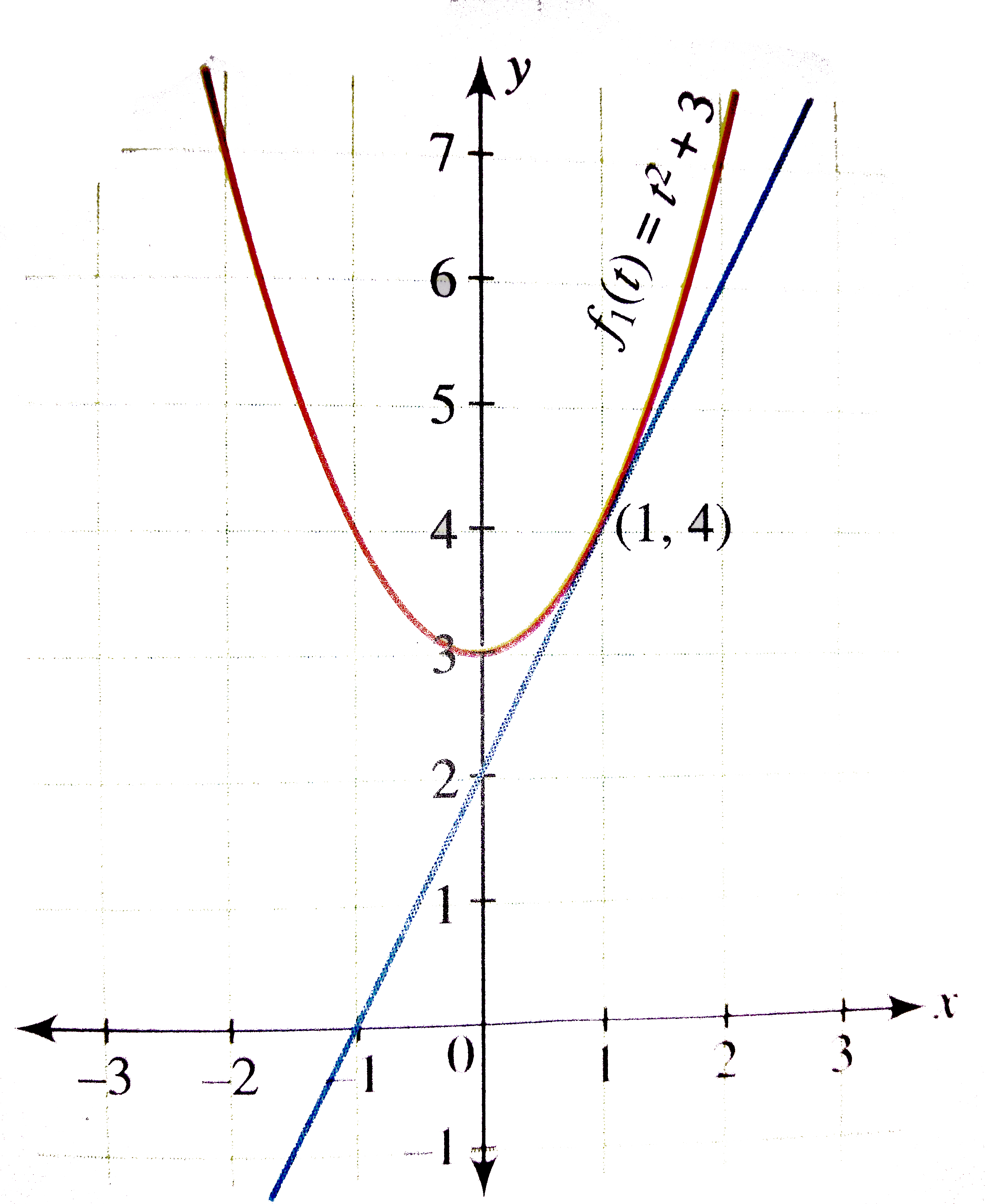
Let f1(t)=t2+3andf2(t)=a(t+1)
(a) For x<0,t∈(0,1). That means (i) should have at least one solution in t∈(0,1).
From (i), it is obvious that a∈R+.
Now f2(t)=a(t+1) represents a straight line. It should meet the curve.
f1(t)=t2+3, at least once in t∈(0,1).
f1(0)=3,f1(0)⇒a=3,iff1(1)=f2(1)=a=2
Hence required a∈(2,3).
(b) For at least one positive solution, t∈(1,∞). That means the graphs of f1(t)=t2+3andf2(t)=a(t+1) should meet at least once in t∈(1,∞).
If a=2, both curves touch each other at (1,4).
Hence required a∈(2,∞).
(c) In this case, both graphs should meet at least once in t∈(0,∞).
For a=2, both curves touch, hence required a∈[2,∞).
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
Similar Questions
Consider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequations has at least one negative solution.
View SolutionConsider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequaiton has at least one positive solution:
View SolutionConsider the inequation x2+x+a−9<0
The value of the parameter a so that the given inequaiton is ture ∀x∈(−1,3)
View SolutionFind the possible values of 'a' such that the inequality 3−x2>|x−a| has atleast one negative solution
View SolutionIf f(x)=t+3x−x2x−4, where t is a parameter that has minimum and maximum, then the range of values of t is (a) (0,4) (b) (0,∞) (c) (−∞,4) (d) (4,∞)
View SolutionThe solution set of the inequation x+4x−3≤2, is
View Solutionf(x)=(x−2)|x−3| is monotonically increasing in (a)(−∞,52)∪(3,∞) (b) (52,∞) (c)(2,∞) (d) (−∞,3)
View SolutionProve that the equation 2sinx=|x|+a has no solution for a∈(3√3−π3,∞).
View SolutionProve that the equation 2sinx=|x|+a has no solution for a∈(3√3−π3,∞).
View SolutionProve that the equation 2sinx=|x|+a has no solution for a∈(3√3−π3,∞).
View Solution