For a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
For P(x,y), we have
2≤d1(P)+d2(P)≤4
⇒ 2≤|x−y|√2+|x+y|√2≤4 ltBrgt ⇒ 2√2≤|x−y|+|x+y|≤4√2
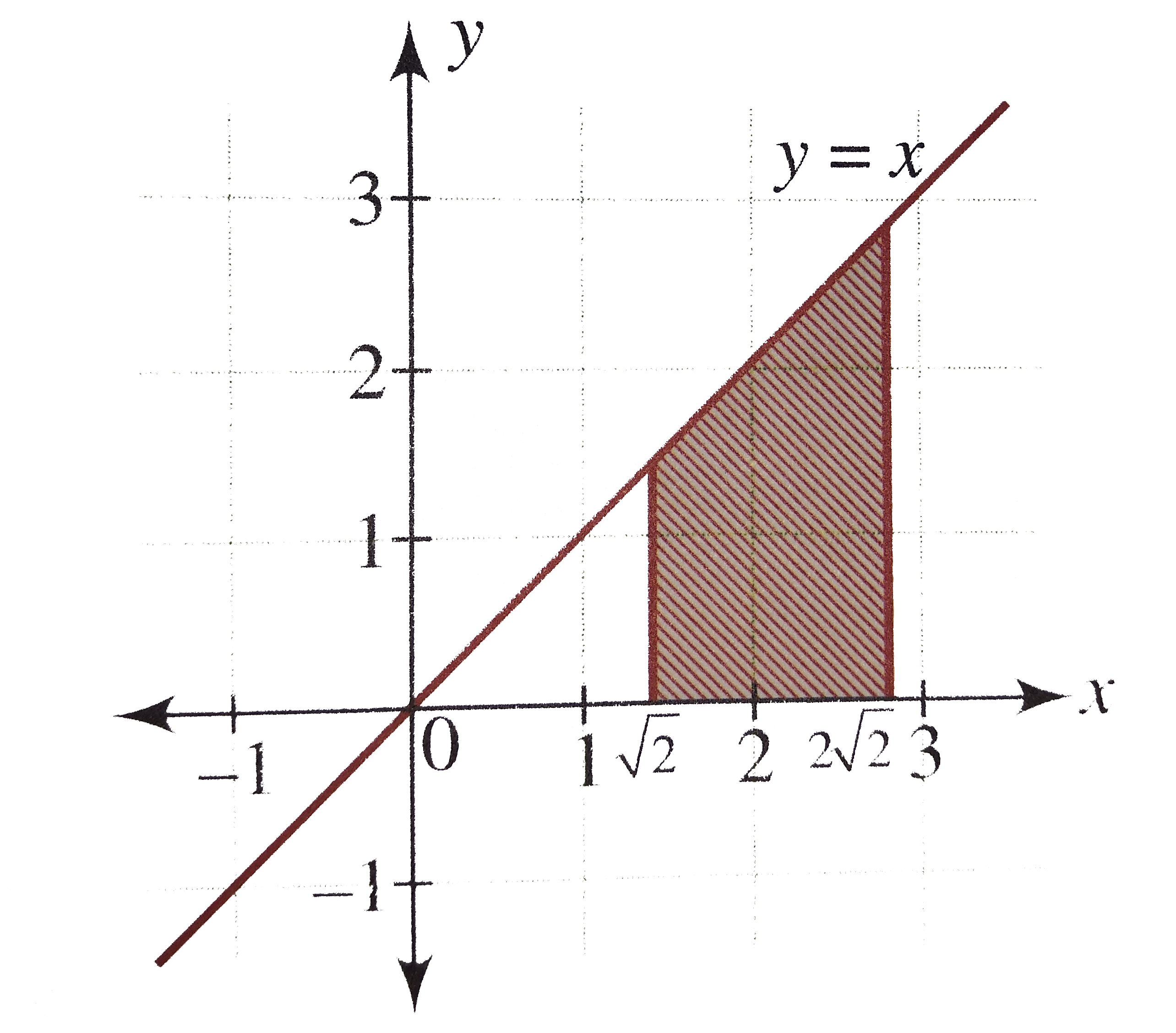
In the first quadrant if x>y, we have
2√2≤x−y+x+y≤4√2
or √2≤x≤2√2
The region of points satisfying these inequalities is as follows.
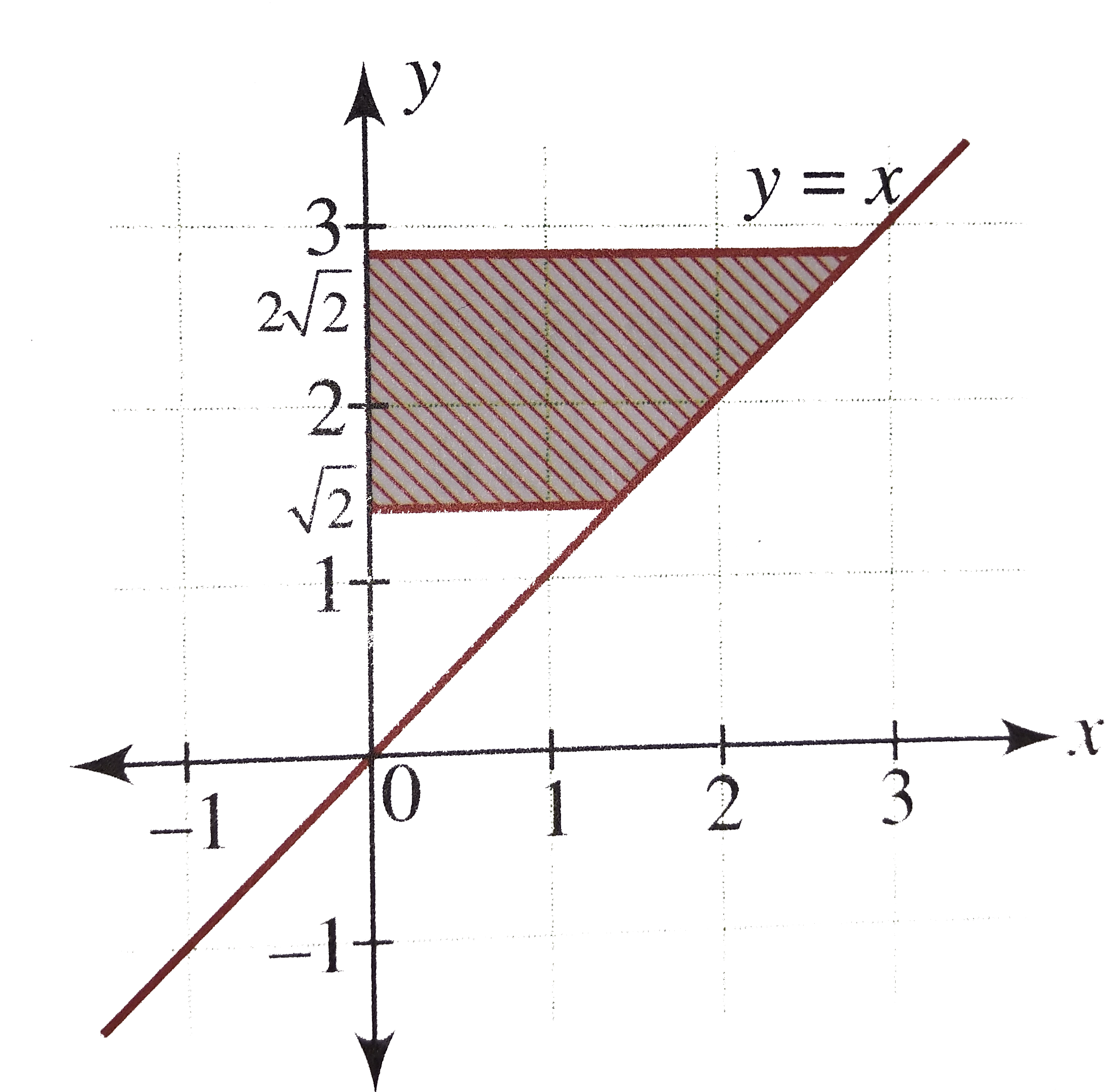
In the first quadrant if x<y, we have
2√2≤y−x+y≤4√2
or √2≤y≤2√2
The region of points satisfying these inequalities is as follows.
Combining the above two regions, we have the following.
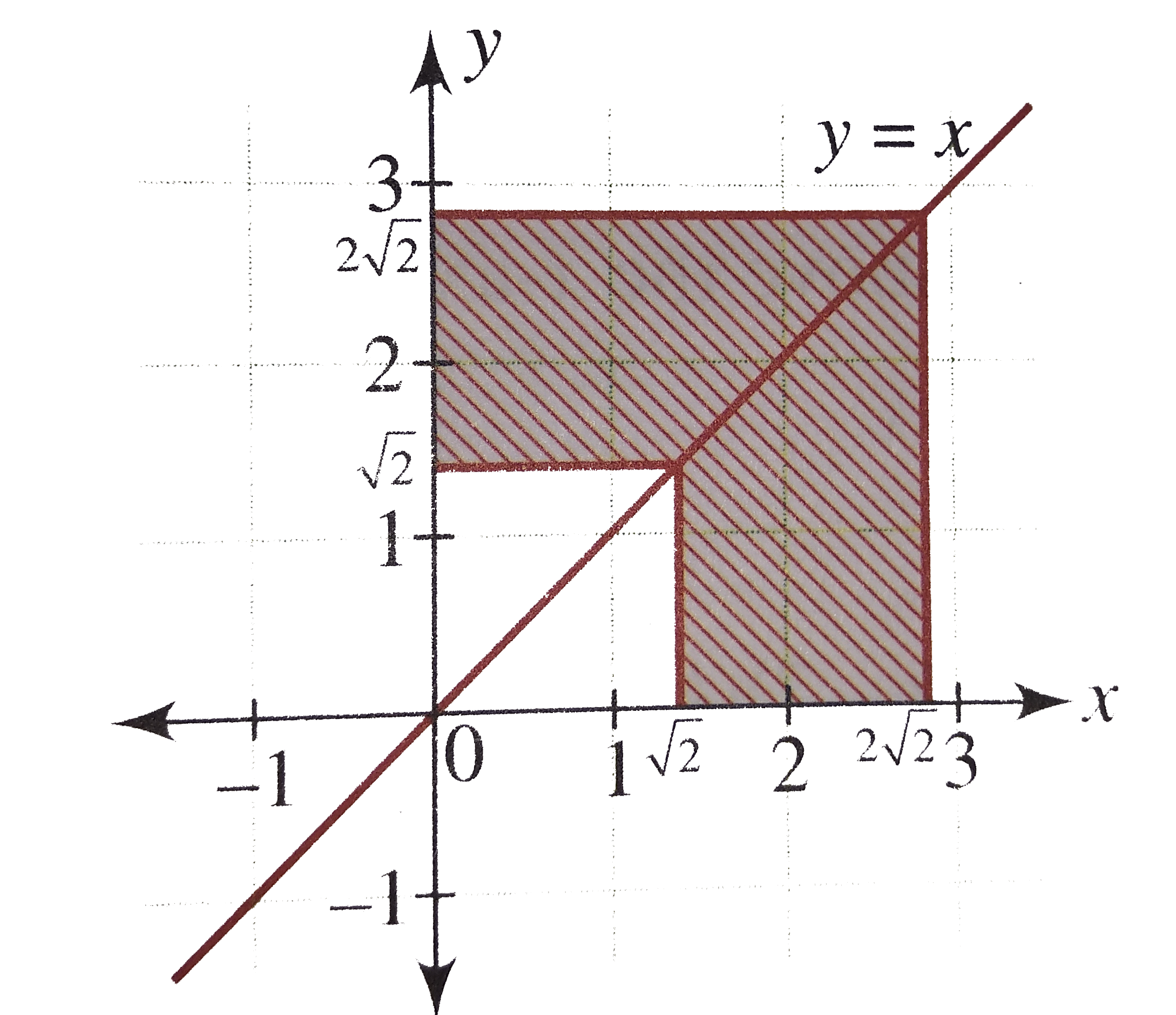
Area of the shaded region =((2√2)2−(√2)2)
=8−2=6 sq.units
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
Similar Questions
Plot the region of the points P (x,y) satisfying |x|+|y|<1.
View SolutionConsider a rectangle ABCD formed by the points A=(0,0), B= (6, 0), C =(6, 4) and D =(0,4), P (x, y) is a moving interior point of the rectangle, moving in such a way that d(P,AB)≤min{d(P,BC),d(P,CD)andd(P,AD)} here d (P, AB), d (P, BC), d (P, CD) and d (P, AD) represent the distance of the point P from the sides AB, BC, CD and AD respectively. Area of the region representing all possible positions of the point P is equal to (a) 8 sq. units (b) 4 sq. units (c) 12 sq. units (d) 6 sq. units
View SolutionFind the distance of the point P(−1,−5,−10) from the point of intersection of the line joining the points A(2,−1,2)andB(5,3,4) with the plane x−y+z=5.
View SolutionLet P be the set of points (x,y) such that x2≤y≤–2x+3. Then area of region bounded by points in set P is
View SolutionLet P be the image of the point (3,1,7) with respect to the plane x−y+z=3. Then, the equation of the plane passing through P and containing the straight line x1=y2=z1 is
View SolutionIf P is any point on the plane lx+my+nz=pandQ is a point on the line OP such that OP.OQ=p2 , then find the locus of the point Q.
View SolutionLet (x,y) be any point on the parabola y2=4x. Let P be the point that divides the line segment from (0,0) and (x,y) n the ratio 1:3. Then the locus of P is :
View SolutionLet (x,y) be any point on the parabola y2=4x. Let P be the point that divides the line segment from (0,0) and (x,y) n the ratio 1:3. Then the locus of P is :
View SolutionIf P is any point on the plane lx+my+nz=pandQ is a point on the line OP such that OP.OQ=p2 , then find the locus of the point Q.
View SolutionLet there are three points A(0,43),B(–1,0) and C(1,0) in x – y plane. The distance from a variable point P to the line BC is the geometic mean of the distances from this point to lines AB and AC then locus of P can be
View Solution
