(a) Show using a proper diagram how unpolarised light can be linearly polarised by reflection from a transparent glass surface.
(b) The figure shows a ray of light falling normally on. the face AB of an equilateral glass prism having refractive index 3/2, placed A in water ofrefractive index 4/3. Will this ray suffer total internal reflection on striking the face AC? Justify your answer.
Solution:
(a) To show how unpolarized light can be linearly polarized by reflection from a transparent glass surface, we can follow these steps:
1. Understanding Unpolarized Light: Unpolarized light consists of waves vibrating in multiple planes. When it strikes a surface, some of the light is reflected and some is refracted.
2. Incident Ray: Draw a diagram with a glass surface and a normal line (perpendicular to the surface). Let the incident ray strike the glass surface at an angle θ.
3. Reflection and Refraction: When the unpolarized light strikes the glass surface, part of it is reflected (reflected ray) and part is refracted (refracted ray).
4. Polarization Condition: For the reflected light to be completely polarized, the angle between the reflected ray and the refracted ray should be 90 degrees. This condition is met when the angle of incidence θ is equal to Brewster's angle (θ_B).
5. Brewster's Angle: Brewster's angle can be calculated using the formula:
\(
\tan(\theta_B) = \frac{n_2}{n_1}
\)
where \(n_1\) is the refractive index of the first medium (air, approximately 1) and \(n_2\) is the refractive index of the glass.
6. Diagram: In the diagram, label the incident ray, reflected ray, refracted ray, and the angles involved. The reflected ray will be polarized in the plane parallel to the surface.
Diagram:
∣∣∣∣∣∣∣ RetedRay∣∣∣∣∣∣∣|⊢−−−−−−− GlassSurface|∣∣∣∣∣∣⌊__________Normal
(b) To determine if the ray will suffer total internal reflection when striking face AC of the prism:
1. Identify the Angles: The ray strikes face AB normally, meaning the angle of incidence at face AB is 0 degrees. The angle of refraction can be calculated using Snell's law:
\(
n_1 \sin(\theta_1) = n_2 \sin(\theta_2)
\)
where \(n_1 = 1\) (water), \(n_2 = \frac{3}{2}\) (glass), and \(\theta_1 = 0\).
2. Calculate Refracted Angle: Since \(\sin(0) = 0\), the ray passes straight through into the glass.
3. Incident Angle at Face AC: The angle of incidence at face AC can be calculated. Since the prism is equilateral, the angle at C is 60 degrees. Thus, the angle of incidence at AC is:
\(
\theta_i = 60^\circ
\)
4. Critical Angle Calculation: To determine if total internal reflection occurs, we need to calculate the critical angle using:
\(
\sin(\theta_c) = \frac{n_2}{n_1}
\)
where \(n_2 = \frac{3}{2}\) (glass) and \(n_1 = \frac{4}{3}\) (water).
5. Finding Critical Angle:
\(
\sin(\theta_c) = \frac{3/2}{4/3} = \frac{9}{8}
\)
Since \(\sin(\theta_c)\) cannot exceed 1, we find that total internal reflection cannot occur.
6. Conclusion: Since the angle of incidence (60 degrees) is less than the critical angle, the ray will not suffer total internal reflection when striking face AC.
\(
\tan(\theta_B) = \frac{n_2}{n_1}
\)
where \(n_1\) is the refractive index of the first medium (air, approximately 1) and \(n_2\) is the refractive index of the glass.
∣∣∣∣∣∣∣ RetedRay∣∣∣∣∣∣∣|⊢−−−−−−− GlassSurface|∣∣∣∣∣∣⌊__________Normal
\(
n_1 \sin(\theta_1) = n_2 \sin(\theta_2)
\)
where \(n_1 = 1\) (water), \(n_2 = \frac{3}{2}\) (glass), and \(\theta_1 = 0\).
\(
\theta_i = 60^\circ
\)
\(
\sin(\theta_c) = \frac{n_2}{n_1}
\)
where \(n_2 = \frac{3}{2}\) (glass) and \(n_1 = \frac{4}{3}\) (water).
\(
\sin(\theta_c) = \frac{3/2}{4/3} = \frac{9}{8}
\)
Since \(\sin(\theta_c)\) cannot exceed 1, we find that total internal reflection cannot occur.
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - A7videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - B7videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - E5videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
A light ray is normally incident onone face of equilateral glass prism of refractive index √2. The deviation of light ray is
View SolutionA glass prism of refractive index 1.5 is immersed in water of refractive index 4/3. A light ray incident normally on face AB is totally reflected at face AC if
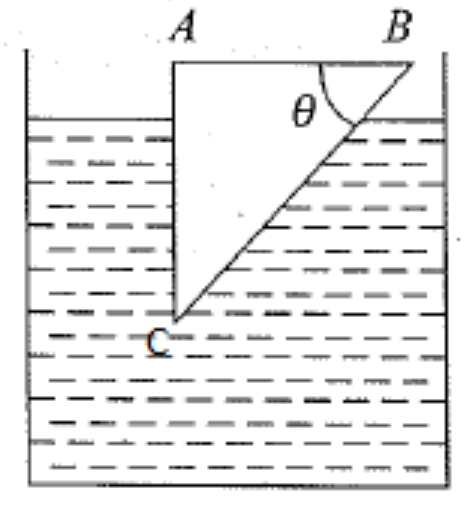 View Solution
View SolutionA glass prism of refractive index 1.5 is immersed in water (refractive index 4/3) . A light beam normally on the face AB is totally reflected to reach on the face BC if
 View Solution
View SolutionA ray of light is incident normally on one face of 30∘−60∘−90∘ prism of refractive index 5/3 immersed in water of refractive index 4/3 as shown in figure .
_E01_076_Q01.png) View Solution
View SolutionA ray of light is incident normally on one face of an equilateral prism of refractive index 1.5. The angle of deviation is: (Given sin−1.23=42∘)
View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionA ray of light incident normally on one face of a right isosceles prism is totally reflected. What must be the minimum value of refractive index of glass ? Give relevant calculations.
View SolutionA equilateral glass prism has a refractive index √2. A light ray is incident at 45∘ on one face. Total deviation of ray is n×15∘ where n is
View SolutionA glass prism is immeresed in water as shown in the figure. When a beam of light incident is incident normally on the face ab, it is internally reflected at the face ad. If the refractive index of glass is 1.5 and that of water is 4/3, then
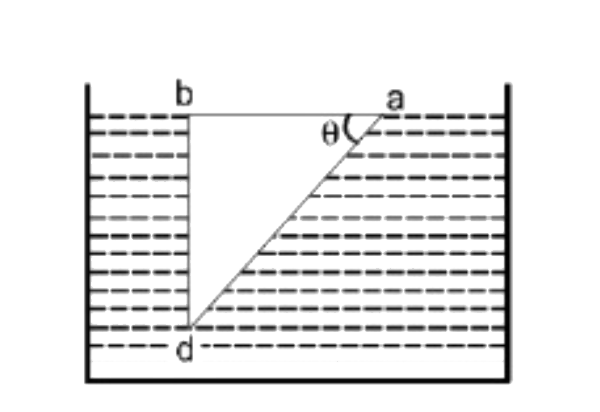 View Solution
View SolutionA trianglular prims of glass is shown in the figure. A ray incident normally to one face is totally reflected. If θ=45∘ the refractive index of glass is
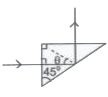 View Solution
View Solution
